Question

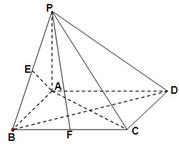在四棱锥P-ABCD中，底面ABCD是矩形，侧棱PA⊥底面ABCD，AB=1，直线PB与底面ABCD所成的角为45°，四棱锥P-ABCD的体积V=

2

3

，E为PB的中点，点F在棱BC上移动．
（1）求证：PF⊥AE；
（2）当F为BC中点时，求点F到平面BDP的距离；
（3）在侧面PAD内找一点G，使GE⊥平面PAC．

Answer 1

分析：方法一：
（1）观察图形可知：BC⊥平面PAB，则PF在平面PAB上的射影是PB，AE⊥PB，所以由三垂线定理得：PF⊥AE
（2）求点到面的距离，常用方法有体积法，作垂线求垂线段的长度．这题由PA⊥底面ABCD可知：三棱锥V_P-BDF=V_F-BDP，体积较易求得，所以这题我们可以考虑用体积法求解
（3）寻找直线与平面垂直，可以通过平面与平面垂直进行转化，平面PAC⊥平面ABCD，平面PAC∩平面ABCD=AC，所以在平面ABCD内，过B作BF⊥AC交AD于F，连接PF，设PF的中点为G，连接GE，则GE∥BF，则GE⊥平面PAC
方法二：
以A为坐标原点，直线AB、AD、AP分别为x、y、z轴，建立空间直角坐标系，设BF=x，则A（0，0，0），B（1，0，0），C（1，2，0），D（0，2，0），P（0，0，1），F（1，x，0），E（

1

2

，0，

1

2

）．这种解法的好处就是：（1）解题过程中较少用到空间几何中判定线线、面面、线面相对位置的有关定理，因为这些可以用向量方法来解决．（2）即使立体感稍差一些的学生也可以顺利解出，因为只需画个草图以建立坐标系和观察有关点的位置即可．

解答：解：
方法一：
（1）∵PA⊥底面ABCD，∠PBA是侧棱PB与底面ABCD所成的角，
∴∠PBA=45°
∵AB=1，∴PA=1
∵V=

1

3

AB*AD*PA=

2

3

∴AD=2，
∵PA⊥底面ABCD
∴PA⊥BC
∵AB⊥BC
∴BC⊥平面PAB
∴PF在平面PAB上的射影是PB
∵AE?平面PAB，AE⊥PB
∴由三垂线定理得：PF⊥AE

（2）设点F到平面BDP的距离为h
则由V_P-BDF=V_F-BDP得：

1

3

S_△BDF*PA=

1

3

S_△BDF*h
∴h=

S△BDF

S△BDP

=

1 2

3 2

=

1

3

（3）在平面ABCD内，过B作BF⊥AC交AD于F，连接PF，设PF的中点为G，连接GE，则GE∥BF．
∵BF⊥AC，BF⊥PA
∴BF⊥平面PAC
∴GE⊥平面PAC

方法二：
（1））∵PA⊥底面ABCD，∠PBA是侧棱PB与底面ABCD所成的角，
∴∠PBA=45°
∵AB=1，∴PA=1
∵V=

1

3

AB*AD*PA=

2

3

∴AD=2，
以A为坐标原点，直线AB、AD、AP分别为x、y、z轴，建立空间直角坐标系，
设BF=x，则A（0，0，0），B（1，0，0），C（1，2，0），D（0，2，0），P（0，0，1），F（1，x，0），E（

1

2

，0，

1

2

）
∵

PF

•

AE

=（1，x，-1）•（

1

2

，0，

1

2

）=0
∴PF⊥AE

（2）∵F为BC的中点
∴F（1，1，0），从而

PF

=（1，1，-1），

BD

=（-1，2，0），

BP

=（-1，0，1），
设平面BDP的法向量为

n

=（a，b，c），则：

n • BD =0 n • BP =0

即

-a+2b=0 -a+c=0

得

a=2b a=c

令b=1得，

n

=（2，1，2）
∴点F到平面BDP的距离为h=

| PF • n |

| n |

=

2+1-2

3

=

1

3

（3）设G（0，m，n），则

GE

=（

1

2

，-m，

1

2

-n）
由GE⊥平面PAC可得

GE • AP =0 GE • AC =0

即

1 2 -n=0 1 2 -2m=0

∴

m= 1 4 n= 1 2

∴满足条件的点为G（0，

1

4

，

1

2

）

点评：本小题主要考查空间线面关系、几何体的体积应用、解三角形等基础知识，考查数形结合、化归与转化的数学思想方法，以及空间想象能力、推理论证能力和运算求解能力．