��Ŀ����
(��������12��)
ij��������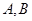 ����Ԫ����������������ָ�껮��Ϊ�����ڻ����7��5Ϊ��Ʒ��С��7��5Ϊ��Ʒ���ִ�һ����Ʒ�������ȡ������Ԫ����5�����м�⣬�������¼���£�
����Ԫ����������������ָ�껮��Ϊ�����ڻ����7��5Ϊ��Ʒ��С��7��5Ϊ��Ʒ���ִ�һ����Ʒ�������ȡ������Ԫ����5�����м�⣬�������¼���£�
|
|
7 |
7 |
7��5 |
9 |
9��5 |
|
|
6 |
|
8��5 |
8��5 |
|
���ڱ�����������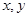 �����壬ͳ��Աֻ�ǵ�
�����壬ͳ��Աֻ�ǵ�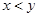 ����
����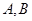 ����Ԫ���ļ�����ݵ�ƽ��ֵ��ȣ�����Ҳ��ȣ�
����Ԫ���ļ�����ݵ�ƽ��ֵ��ȣ�����Ҳ��ȣ�
�����������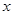 ��
��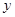 ��ֵ��
��ֵ��
�������ӱ�����5��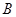 ��Ԫ������ȡ2������2����Ϊ��Ʒ�ĸ��ʣ�
��Ԫ������ȡ2������2����Ϊ��Ʒ�ĸ��ʣ�
����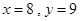 ����
����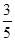
��������
���������(��)��Ϊ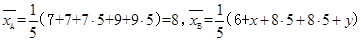 ��
��
�� ����
���� �� �� 2����Ϊ
�� �� 2����Ϊ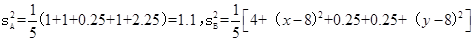 ��
��
��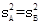 ����
����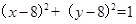 �� �� 4��
�� �� 4��
�ɢ٢ڽ��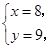 ��
��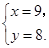
��Ϊ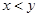 ��
��
����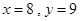 ��
6��
��
6��
(��) �DZ�����5��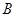 ��Ԫ���ֱ�Ϊ
��Ԫ���ֱ�Ϊ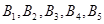 ������
������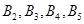 Ϊ��Ʒ��
Ϊ��Ʒ��
������ȡ2��,����10�������¼����о�����:
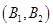 ��
��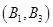 ��
��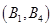 ��
��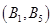 ��
��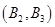 ��
��
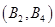 ��
��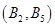 ��
��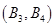 ��
��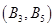 ��
��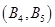 ��
8��
��
8��
�ǡ�2����Ϊ��Ʒ��Ϊ�¼�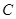 �����¼�
�����¼�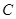 ��������6�������¼���
��������6�������¼���
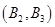 ��
��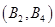 ��
��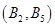 ��
��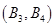 ��
��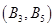 ��
��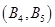 .
10��
.
10��
����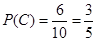 ����2����Ϊ��Ʒ�ĸ���Ϊ
����2����Ϊ��Ʒ�ĸ���Ϊ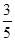 . 12��
. 12��
���㣺��С����Ҫ����ŵ���͡�ͳ�ƵȻ���֪ʶ���������ݴ���������������������Լ�Ӧ����ʶ��
���������ŵ������ʱ��Ҫ��֤ÿ�������¼������Ŀ��������.

 �߽�������ϵ�д�
�߽�������ϵ�д�