题目内容
若点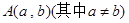 在矩阵
在矩阵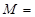
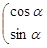
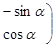 对应变换的作用下得到的点为
对应变换的作用下得到的点为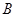
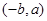 ,(Ⅰ)求矩阵
,(Ⅰ)求矩阵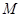 的逆矩阵;
的逆矩阵;
(Ⅱ)求曲线C:x2+y2=1在矩阵N=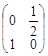 所对应变换的作用下得到的新的曲线C'的方程.
所对应变换的作用下得到的新的曲线C'的方程.
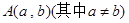 在矩阵
在矩阵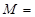
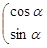
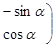 对应变换的作用下得到的点为
对应变换的作用下得到的点为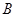
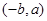 ,(Ⅰ)求矩阵
,(Ⅰ)求矩阵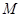 的逆矩阵;
的逆矩阵;(Ⅱ)求曲线C:x2+y2=1在矩阵N=
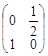 所对应变换的作用下得到的新的曲线C'的方程.
所对应变换的作用下得到的新的曲线C'的方程.(Ι)
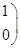 (Ⅱ)
(Ⅱ)

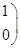 (Ⅱ)
(Ⅱ)
本题主要考查矩阵乘法、逆矩阵与变换等基本知识.
本小题可知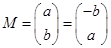 ,即
,即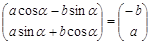 ,从而得到
,从而得到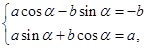 求出M.然后根据
求出M.然后根据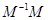 ,求出M的逆矩阵.
,求出M的逆矩阵.
参照(1)的解题思路去解即可.
(Ι)法一: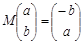 ,即
,即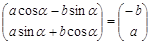 ,……………………1分
,……………………1分
所以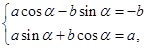 得
得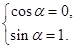 ……………………3分
……………………3分
即M=
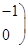 ,由
,由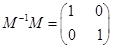 得
得
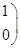 . ………………4分
. ………………4分
法二:同法一可求得M=
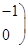 因为
因为
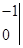 =1
=1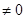 ,
,
 . …4分
. …4分
(Ⅱ)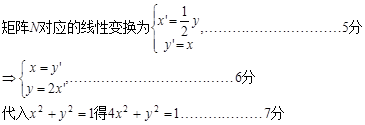
本小题可知
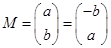 ,即
,即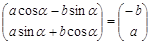 ,从而得到
,从而得到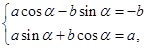 求出M.然后根据
求出M.然后根据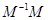 ,求出M的逆矩阵.
,求出M的逆矩阵.参照(1)的解题思路去解即可.
(Ι)法一:
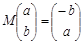 ,即
,即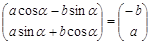 ,……………………1分
,……………………1分所以
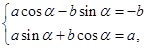 得
得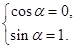 ……………………3分
……………………3分即M=

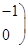 ,由
,由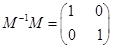 得
得
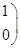 . ………………4分
. ………………4分法二:同法一可求得M=

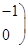 因为
因为
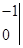 =1
=1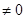 ,
,
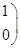 . …4分
. …4分(Ⅱ)

练习册系列答案
相关题目

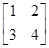 ,N=
,N=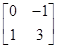 .
.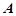 的逆矩阵
的逆矩阵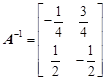 ,求矩阵
,求矩阵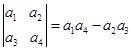 .若将函数
.若将函数 的图象向左平移
的图象向左平移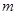
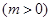 个单位后,所得图象对应的函数为奇函数,则
个单位后,所得图象对应的函数为奇函数,则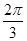
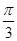
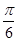
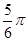
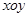 中,点
中,点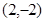 在矩阵
在矩阵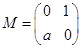 对应变换作用下得到点
对应变换作用下得到点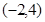 ,曲线
,曲线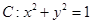 在矩阵
在矩阵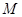 对应变换作用下得到曲线
对应变换作用下得到曲线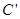 ,求曲线
,求曲线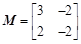 ,
,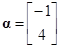 ,试计算:
,试计算: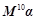 .
.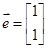 ,并且矩阵M对应的变换将点
,并且矩阵M对应的变换将点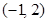 变成点
变成点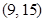 ,求出矩阵M.
,求出矩阵M.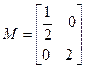 ,矩阵M对应的变换把曲线
,矩阵M对应的变换把曲线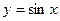 变为曲线C,求曲线C的方程。
变为曲线C,求曲线C的方程。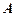
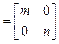 ,若矩阵
,若矩阵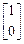 ,属于特征值2的一个特征向量为
,属于特征值2的一个特征向量为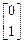 ,求实数
,求实数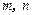 的值
的值