题目内容
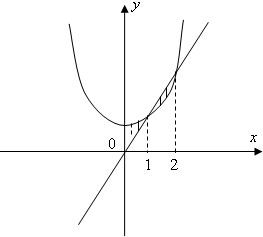
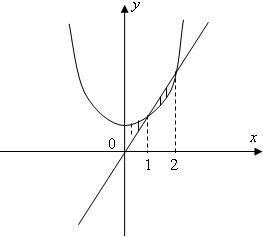
求由曲线y=x2+2与y=3x，x=0，x=2所围成的平面图形的面积．
【答案】分析：因为所求区域均为曲边梯形，所以使用定积分方可求解．
解答：解：联立
，解得x1=1，x2=2
∴S=∫1（x2+2-3x）dx+∫12（3x-x2-2）dx=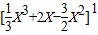
+
=1
点评：用定积分求面积时，要注意明确被积函数和积分区间，属于基本运算．
解答：解：联立
，解得x1=1，x2=2∴S=∫1（x2+2-3x）dx+∫12（3x-x2-2）dx=
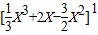+=1点评：用定积分求面积时，要注意明确被积函数和积分区间，属于基本运算．
练习册系列答案
名题金卷系列答案
相关题目
