题目内容
20．函数f（x）=$\frac{{x}^{2}-x}{2x+1}$，当x＞1时的值域是（0，+∞）．分析 求导数f′（x）=$\frac{2{x}^{2}+2x-1}{（2x+1）^{2}}$，根据二次函数的单调性可以判断2x2+2x-1＞0，从而得出函数f（x）在（1，+∞）上单调递增，从而f（x）＞f（1），这便求出了原函数的值域．
解答 解：$f′（x）=\frac{2{x}^{2}+2x-1}{（2x+1）^{2}}$；
设g（x）=2x2+2x-1，g（x）对称轴为x=$-\frac{1}{2}$，∴在（1，+∞）上单调递增；
∴g（x）＞g（1）=3＞0；
∴f′（x）＞0；
∴f（x）在（1，+∞）上单调递增；
∴f（x）＞f（1）=0；
∴函数f（x）的值域为（0，+∞）．
故答案为：（0，+∞）．
点评 考查函数值域的概念，根据导数符号判断函数单调性的方法，根据二次函数的单调性求值域，要正确求导．
练习册系列答案
百年学典课时学练测系列答案
相关题目
5．过极点，从极轴到直线l的角为$\frac{2π}{3}$的射线的极坐标方程为（ ）
| A． | θ=$\frac{2π}{3}$ | B． | θ=$\frac{2π}{3}$（ρ≥0） | C． | θ=$\frac{2π}{3}$（ρ∈R） | D． | θ=$\frac{5π}{3}$（ρ≥0） |
12．圆x2+y2-4x+6y=0截x轴与截y轴所得的弦长之比为（ ）
| A． | $\frac{4}{9}$ | B． | $\frac{9}{4}$ | C． | $\frac{3}{2}$ | D． | $\frac{2}{3}$ |
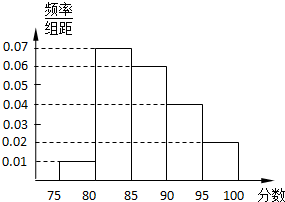某高校在2013年考试成绩中随机抽取100名学生的笔试成绩，按成绩分组：第1组[75，80），第2组[80，85），第3组[85，90），第4组[90，95），第5组[95，100]得到的频率分布直方图如图所示，