题目内容
已知数列 满足
满足 ,
, ,则该数列的通项公式
,则该数列的通项公式
 满足
满足 ,
, ,则该数列的通项公式
,则该数列的通项公式
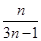
试题分析:由
 得:
得: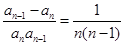 ,化为
,化为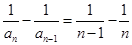 ,所以
,所以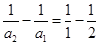 ,
,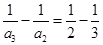 ,
,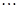 ,
,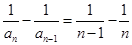 ,各式相加得:
,各式相加得: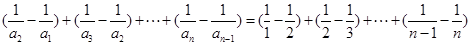 ,化为
,化为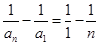 ,因为
,因为 ,所以
,所以
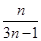 。
。点评:对于求一般数列的通项公式或前n项和时,常用方法有:错位相减法、裂变法等,目的是消去中间部分。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
 满足
满足 ,
, ,则该数列的通项公式
,则该数列的通项公式
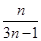
 得:
得: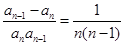 ,化为
,化为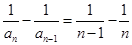 ,所以
,所以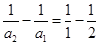 ,
,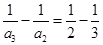 ,
,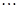 ,
,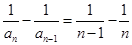 ,各式相加得:
,各式相加得: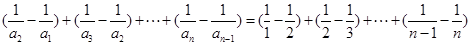 ,化为
,化为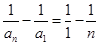 ,因为
,因为 ,所以
,所以
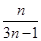 。
。
 阅读快车系列答案
阅读快车系列答案