题目内容
11.已知x,y为正数,且x+y=2,则$\frac{2}{x}$+$\frac{1}{y}$的最小值为( )| A. | 2 | B. | $\frac{3}{2}$+$\sqrt{2}$ | C. | $\sqrt{2}$ | D. | 2-$\sqrt{2}$ |
分析 把x+y=2变形为$\frac{x}{2}+\frac{y}{2}=1$,代入$\frac{2}{x}$+$\frac{1}{y}$后展开,然后利用基本不等式求最值.
解答 解:∵x,y为正数,且x+y=2,则$\frac{x}{2}+\frac{y}{2}=1$,
∴$\frac{2}{x}$+$\frac{1}{y}$=($\frac{x}{2}+\frac{y}{2}$)($\frac{2}{x}$+$\frac{1}{y}$)=1+$\frac{1}{2}$+$\frac{x}{2y}+\frac{y}{x}$$≥\frac{3}{2}+2\sqrt{\frac{x}{2y}•\frac{y}{x}}=\frac{3}{2}+\sqrt{2}$.
当且仅当$x=4-2\sqrt{2},y=2\sqrt{2}-2$时上式“=”成立.
故选:B.
点评 本题考查基本不等式,训练了利用基本不等式求最值,利用基本不等式求函数最值要注意:“一正、二定、三相等”,是基础题.

练习册系列答案
相关题目
1.sin(-135°)的值是( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{{\sqrt{2}}}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
19.已知集合A={x|x2-2x≤0},B={x|x<m},若A⊆B,则实数m的取值范围是( )
| A. | [2,+∞) | B. | (2,+∞) | C. | (-∞,0) | D. | (-∞,0] |
3.已知点A是圆C:x2+y2+ax+4y+30=0上任意一点,A关于直线x+2y-1=0的对称点也在圆C上,则实数a的值( )
| A. | 10 | B. | -10 | C. | 4 | D. | -4 |
20.若函数f(x)=$\left\{\begin{array}{l}{{a}^{x},x>1}\\{(4-\frac{a}{2})x+2,x≤1}\end{array}\right.$是R上的增函数,则实数a的取值范围为 ( )
| A. | (1,+∞) | B. | (1,8) | C. | (4,8) | D. | [4,8) |
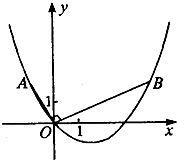 如图,在平面直角坐标系中,OB⊥OA,且OB=2OA,点A的坐标 是(-1,2)
如图,在平面直角坐标系中,OB⊥OA,且OB=2OA,点A的坐标 是(-1,2)