题目内容
圆x2+y2+4y=0与直线3x+4y+2=0相交于A、B两点,则线段AB的垂直平分线的方程是( )
| A.4x-3y-6=0 | B.4x+3y+6=0 | C.3x+4y+8=0 | D.4x-3y-2=0 |
由直线和圆的位置关系可得:
线段AB的垂直平分线是垂直于直线3x+4y+2=0且过圆心(0,-2)的直线,
由直线的垂直关系可得所求直线的向量为
,
故方程为:y-(-2)=
(x-0),即4x-3y-6=0
故选A
线段AB的垂直平分线是垂直于直线3x+4y+2=0且过圆心(0,-2)的直线,
由直线的垂直关系可得所求直线的向量为
| 4 |
| 3 |
故方程为:y-(-2)=
| 4 |
| 3 |
故选A

练习册系列答案
相关题目
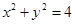 与圆
与圆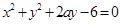 (
(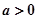 )的公共弦长为
)的公共弦长为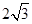 ,则
,则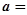 _____.
_____. 的位置关系是( )
的位置关系是( )