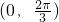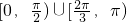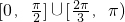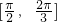题目内容
如果y=f（x）的导函数的图象是开口向上，顶点坐标为（1，-
），那么曲线y=f（x）上任一点的切线的倾斜角α的取值范围是（ ）
| 3 |
分析：由二次函数的图象可知最小值为-
，再根据导数的几何意义可知k=tanα≥-
，结合正切函数的图象求出角α的范围．
| 3 |
| 3 |
解答：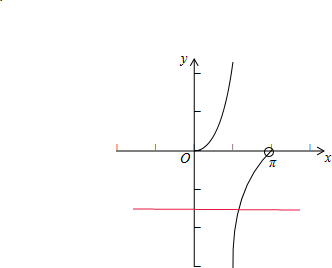
解：由题意可知f′（x）≥-
，即tanα≥-
结合正切函数的图象，其中红色线为y=-
可得α∈[0，
)∪[
，π)
故选B
解：由题意可知f′（x）≥-| 3 |
| 3 |
结合正切函数的图象，其中红色线为y=-
| 3 |
可得α∈[0，
| π |
| 2 |
| 2π |
| 3 |
故选B
点评：本题考查导数的几何意义，以及利用正切函数的图象求倾斜角的范围，属基础题．
练习册系列答案
全能练考卷系列答案
相关题目
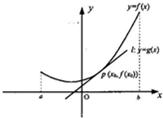
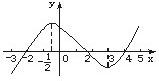
），那么曲线y=f（x）上任一点的切线的倾斜角α的取值范围是
函数y=f（x）在区间
内单调递增；
函数y=f（x）在区间
内单调递减；
时，函数y=f（x）有极大值.