题目内容
如果函数y=f(x)的导函数的图象如图所示,给出下列判断: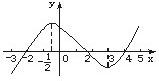
①函数y=f(x)在区间(-3,-
| 1 |
| 2 |
②函数y=f(x)在区间(-
| 1 |
| 2 |
③函数y=f(x)在区间(4,5)内单调递增;
④当x=2时,函数y=f(x)有极小值;
⑤当x=-
| 1 |
| 2 |
则上述判断中正确的是
分析:利用使f′(x)>0的区间是增区间,使f′(x)<0的区间是减区间,分别对①②③进行逐一判定,导数等于零的值是极值,先增后减是极大值,先减后增是极小值,再对④⑤进行判定.
解答:解:①函数y=f(x)在区间(-3,-
)内有增有减,故不正确
②函数y=f(x)在区间(-
,3)有增有减,故不正确
③函数y=f(x)当x∈(4,5)时,恒有f′(x)>0.正确
④当x=2时,函数y=f(x)有极大值,故不正确
⑤当x=-
时,f′(x)≠0,故不正确,
故答案为③
| 1 |
| 2 |
②函数y=f(x)在区间(-
| 1 |
| 2 |
③函数y=f(x)当x∈(4,5)时,恒有f′(x)>0.正确
④当x=2时,函数y=f(x)有极大值,故不正确
⑤当x=-
| 1 |
| 2 |
故答案为③
点评:本题考查了通过导函数图象判定原函数的单调性,以及极值问题,属于易错题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
