题目内容
设函数f(x)=sin( x+
x+ )+cos(
)+cos( x+
x+ )(
)( >0,|
>0,| |<
|< )的最小正周期为π,且f(-x)=f(x),则( )
)的最小正周期为π,且f(-x)=f(x),则( )
A.y="f(x)" 在(0, )单调递减 )单调递减 |
B.y=f(x)在( , , )单调递减 )单调递减 |
C.y=f(x)在(0, )单调递增 )单调递增 |
D.y=f(x)在( , , )单调递增 )单调递增 |
A
解析∵函数f(x) 的最小正周期为π,∴ =2
=2
∴f(x)= sin(2x+
sin(2x+ +
+ )
)
又f(-x)=f(x),所以f(x)为偶函数,即x=0时,f(x)= ,∴
,∴ +
+ =
= (k∈Z)
(k∈Z)
又| |〈
|〈 ,∴
,∴ =
=
∴f(x)= sin(2x+
sin(2x+ +
+ ) =
) = cos2x,不难知道,y="f(x)" 在(0,
cos2x,不难知道,y="f(x)" 在(0, )单调递减
)单调递减

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
已知函数f(x)= ,若
,若 ,则a的取值范围是( )
,则a的取值范围是( )
A. |
B. |
| C.[-2,1] |
| D.[-2,0] |
函数 的递增区间是( )
的递增区间是( )
A.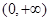 | B. | C. | D. |
 是定义在
是定义在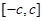 上的奇函数,其图象如图所示,令
上的奇函数,其图象如图所示,令 ,则下列关于函数
,则下列关于函数 的叙述正确的是()
的叙述正确的是()
A.若 ,则函数 ,则函数 的图象关于原点对称 的图象关于原点对称 |
B.若 ,则方程 ,则方程 有大于2的实根 有大于2的实根 |
C.若 ,则方程 ,则方程 有两个实根 有两个实根 |
D.若 ,则方程 ,则方程 有两个实根 有两个实根 |
设动直线 与函数
与函数 的图象分别交于点M、N,则|MN|的最小值为( )
的图象分别交于点M、N,则|MN|的最小值为( )
A. |
B. |
C. |
D. |
函数 的定义域是( )
的定义域是( )
A. |
B. |
C. |
D. |
设 为定义在R上的奇函数,当
为定义在R上的奇函数,当 时,
时, (b为常数),则
(b为常数),则 ( )
( )
| A.3 |
| B.1 |
C. |
D. |
函数 是奇函数的充要条件是
是奇函数的充要条件是
A. | B. | C. | D. |

 的图象大致是( )
的图象大致是( )