题目内容
15.若x∈(0,$\frac{π}{2}$),$y∈(0,\frac{π}{2})$,且tan2x=3tan(x-y),则x+y的可能取值是( )| A. | $\frac{π}{12}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{7π}{12}$ |
分析 先求出x+y的范围,设tan(x-y)=u,得到 w=tan(x+y)=$\frac{2u}{1+{3u}^{2}}$,从而求出tan(x+y)的范围即可.
解答 解:∵x∈(0,$\frac{π}{2}$),y∈(0,$\frac{π}{2}$),∴0<x+y<π.
设tan(x-y)=u,x-y∈(-$\frac{π}{2}$,$\frac{π}{2}$),则u的值域是R,
∵tan2x=3tan(x-y)=3u,
∴tan(x+y)=tan[2x-(x-y)]=$\frac{tan2x-tan(x-y)}{1+tan2xtan(x-y)}$=$\frac{3u-u}{1+{3u}^{2}}$=$\frac{2u}{1+{3u}^{2}}$,
记为 w=tan(x+y)=$\frac{2u}{1+{3u}^{2}}$,
u=0时,w=tan(x+y)=0,
u≠0时:
|w|=$\frac{2|u|}{1+{3|u|}^{2}}$=$\frac{2}{\frac{1}{|u|}+3|u|}$≤$\frac{2}{2\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,当期仅当|u|=$\frac{\sqrt{3}}{3}$时,取等号.
∴-$\frac{\sqrt{3}}{3}$≤tan(x+y)≤$\frac{\sqrt{3}}{3}$,
∴0<x+y≤$\frac{π}{6}$或$\frac{5π}{6}$≤x+y<π,
故选:A.
点评 本题考查了三角函数问题,设tan(x-y)=u,得到w=tan(x+y)=$\frac{2u}{1+{3u}^{2}}$是解题的关键,本题是一道中档题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
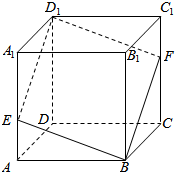 已知E,F分别是正方体A1B1C1D1-ABCD的棱AA1,CC1上的点,且A1E=2EA,CF=2FC1,求证:四边形BED1F是平行四边形.
已知E,F分别是正方体A1B1C1D1-ABCD的棱AA1,CC1上的点,且A1E=2EA,CF=2FC1,求证:四边形BED1F是平行四边形.