题目内容
已知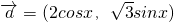 ,
,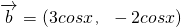 ,设
,设 ,
,
(1)当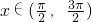 时,求f(x)的最小值及取得最小值时x的取值集合;
时,求f(x)的最小值及取得最小值时x的取值集合;
(2)若锐角α满足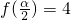 ,求
,求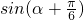 的值.
的值.
解:( 1)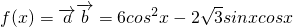
即: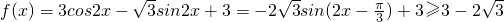 ,
,
此时: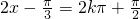 (k∈Z),解得:
(k∈Z),解得: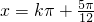 (k∈Z).
(k∈Z).
即f(x)的最小值是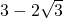 ,此时x的取值集合是
,此时x的取值集合是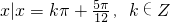 ;
;
( 2)由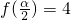 得,
得,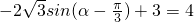 ,
,
即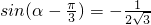 ,
,
因为α是锐角,所以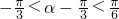 ,
,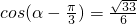 ,
,
所以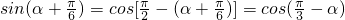 =
=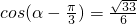
分析:(1)利用函数 .化简函数为一个角的一个三角函数的形式,根据正弦函数的值域,直接求出函数f(x)的最小值及取得最小值时x的取值集合;
.化简函数为一个角的一个三角函数的形式,根据正弦函数的值域,直接求出函数f(x)的最小值及取得最小值时x的取值集合;
(2)根据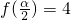 ,求出
,求出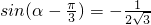 ,利用同角三角函数基本关系式求出
,利用同角三角函数基本关系式求出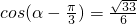 ,利用诱导公式即可求出结果.
,利用诱导公式即可求出结果.
点评:本题考查向量数量积的运算律、三角函数的平方关系和商数关系、三角函数的有界性和最值,考查运算能力,注意在解决三角函数的有关问题时,注意角之间的关系,属中档题.
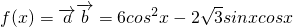
即:
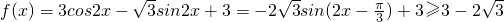 ,
,此时:
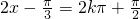 (k∈Z),解得:
(k∈Z),解得: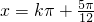 (k∈Z).
(k∈Z).即f(x)的最小值是
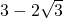 ,此时x的取值集合是
,此时x的取值集合是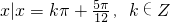 ;
;( 2)由
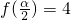 得,
得,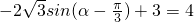 ,
,即
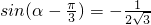 ,
,因为α是锐角,所以
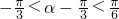 ,
,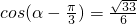 ,
,所以
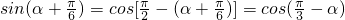 =
=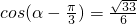
分析:(1)利用函数
 .化简函数为一个角的一个三角函数的形式,根据正弦函数的值域,直接求出函数f(x)的最小值及取得最小值时x的取值集合;
.化简函数为一个角的一个三角函数的形式,根据正弦函数的值域,直接求出函数f(x)的最小值及取得最小值时x的取值集合;(2)根据
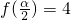 ,求出
,求出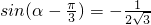 ,利用同角三角函数基本关系式求出
,利用同角三角函数基本关系式求出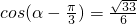 ,利用诱导公式即可求出结果.
,利用诱导公式即可求出结果.点评:本题考查向量数量积的运算律、三角函数的平方关系和商数关系、三角函数的有界性和最值,考查运算能力,注意在解决三角函数的有关问题时,注意角之间的关系,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知椭圆C1:
已知椭圆C1: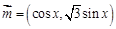 ,
,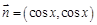 ,设
,设 .
.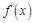 的图像的对称轴及其单调递增区间;
的图像的对称轴及其单调递增区间;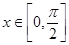 ,求函数
,求函数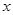 的值;
的值; 分别是锐角
分别是锐角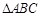 的内角
的内角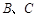 的对边,且
的对边,且 ,
,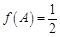 ,试求
,试求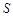 .
. ,a=
,a= .
. 时,求b的值;
时,求b的值;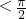 ),求函数f(x)=b+4
),求函数f(x)=b+4
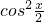 的值域.
的值域. ,a=
,a=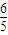 .
.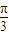 时,求b的值;
时,求b的值;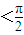 ),求函数f(x)=b+4
),求函数f(x)=b+4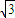
 的值域.
的值域.