题目内容
14.已知数列{an}的前n项和为Sn=3-an-($\frac{1}{2}$)n-1(n∈N*).(1)令bn=2nan,求证:{bn}是等差数列;
(2)令cn=($\frac{2n-1}{n+1}$)an,求数列{cn}的前8项和T8.
分析 (1)利用数列的递推关系,结合等差数列的定义利用构造复数即可证明{bn}是等差数列;
(2)求出cn=($\frac{2n-1}{n+1}$)an的通项公式,利用错位相减法进行求和即可.
解答 证明:(1)∵Sn=3-an-($\frac{1}{2}$)n-1(n∈N*).
∴当n≥2时,Sn-1=3-an-1-($\frac{1}{2}$)n-2(n∈N*).
两式作差得Sn-Sn-1=3-an-($\frac{1}{2}$)n-1-[3-an-1-($\frac{1}{2}$)n-2]=($\frac{1}{2}$)n-1+an-1-an,
即2an=($\frac{1}{2}$)n-1+an-1,
等式两边同时乘以2n-1,得2nan=1+2n-1an-1,
即bn=1+bn-1,
则bn-bn-1=1,故{bn}是等差数列;
解:(2)当n=1时,S1=3-a1-1.
即a1=1.
∵{bn}是等差数列,公差d=1,首项为2a1=2,
∴bn=2nan=2+n-1=n+1,
则an=$\frac{n+1}{{2}^{n}}$,
则cn=($\frac{2n-1}{n+1}$)an=($\frac{2n-1}{n+1}$)$\frac{n+1}{{2}^{n}}$=$\frac{2n-1}{{2}^{n}}$,
则数列{cn}的前8项和T8=$\frac{1}{2}$+$\frac{3}{{2}^{2}}$+$\frac{5}{{2}^{3}}+…+\frac{15}{{2}^{8}}$,
则$\frac{1}{2}$T8=$\frac{1}{{2}^{2}}$+$\frac{3}{{2}^{3}}$+$\frac{5}{{2}^{4}}$+$…+\frac{13}{{2}^{8}}$+$\frac{15}{{2}^{9}}$,
两式作差得$\frac{1}{2}$T8=$\frac{1}{2}$$+\frac{2}{{2}^{2}}$+$\frac{2}{{2}^{3}}+\frac{2}{{2}^{4}}+…+\frac{2}{{2}^{8}}$-$\frac{15}{{2}^{9}}$=$\frac{1}{2}$+$\frac{1}{2}$+$\frac{1}{{2}^{2}}+…+$$\frac{1}{{2}^{7}}$-$\frac{15}{{2}^{9}}$=$\frac{1}{2}$+$\frac{\frac{1}{2}[1-(\frac{1}{2})^{7}]}{1-\frac{1}{2}}$-$\frac{15}{{2}^{9}}$
=$\frac{1}{2}$+1-($\frac{1}{2}$)7-$\frac{15}{{2}^{9}}$=$\frac{3}{2}$-($\frac{1}{2}$)7-$\frac{15}{{2}^{9}}$,
则T8=3-$(\frac{1}{2})^{6}-\frac{15}{{2}^{8}}$.
点评 本题主要考查等差数列的证明以及数列的求和,利用错位相减法是解决数列求和的一种基本方法,考查学生的运算能力.

| A. | [2kπ,2kπ+$\frac{π}{2}$],k∈Z | B. | [2kπ+$\frac{π}{2}$,(2k+1)π],k∈Z | ||
| C. | [2kπ+$\frac{π}{4}$,2kπ+$\frac{3π}{4}$],k∈Z | D. | [2kπ+$\frac{3π}{4}$,2kπ+$\frac{5π}{4}$],k∈Z |
| x | 2 | 4 | 5 | 6 | 8 |
| y | 25 | 35 | m | 55 | 75 |
| A. | 50 | B. | 55 | C. | 60 | D. | 65 |
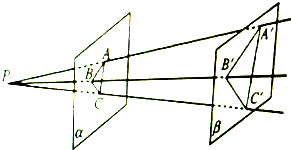 如图,从平面ABC外一点P,引射线PA、PB、PC,在它们上面分别取点A′、B′、C′,使$\frac{PA}{PA′}$=$\frac{PB}{PB′}$=$\frac{PC}{PC′}$,求证:平面ABC∥平面A′B′C′.
如图,从平面ABC外一点P,引射线PA、PB、PC,在它们上面分别取点A′、B′、C′,使$\frac{PA}{PA′}$=$\frac{PB}{PB′}$=$\frac{PC}{PC′}$,求证:平面ABC∥平面A′B′C′.