题目内容
【题目】设抛物线
的焦点为
，点
在抛物线
上，
.若以
为直径的圆过点
，则抛物线的焦点到准线距离为（ ）
A. 8B. 4或8C. 2D. 2或4
【答案】C
【解析】
求得抛物线的焦点和准线方程，运用抛物线的定义和直线和圆相切的条件，求出点M的坐标，代入抛物线方程得p即为答案.
∵抛物线C方程为y2＝2px（p＞0），∴焦点F（
，0），准线方程为x＝﹣，
设M（x，y），由抛物线性质得|MF|＝x+＝2，可得x＝2﹣，
因为圆心是MF的中点，根据中点坐标公式可得，
圆心横坐标为
，
已知圆半径也为1，该圆与y轴相切于点（0，1），
故圆心纵坐标为1，则M点纵坐标为2，
即M（2﹣，2），代入抛物线方程得p2﹣4p+4＝0，解得p＝2，
则C的焦点到准线距离为2．
故选：C．
【题目】近期，某公交公司分别推出支付宝和微信扫码支付乘车活动，活动设置了一段时间的推广期，由于推广期内优惠力度较大，吸引越来越多的人开始使用扫码支付．某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次，用
表示活动推出的天数，
表示每天使用扫码支付的人次（单位：十人次），统计数据如表1所示：表1：
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 6 | 11 | 21 | 34 | 66 | 101 | 196 |
根据以上数据，绘制了如图所示的散点图．
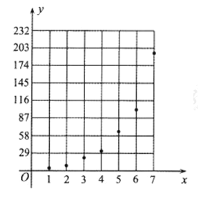
（1）根据散点图判断，在推广期内，
与
均为大于零的常数）哪一个适宜作为扫码支付的人次关于活动推出天数的回归方程类型？（给出判断即可，不必说明理由）；
（2）根据（1）的判断结果及表l中的数据，求关于的回归方程，并预测活动推出第8天使用扫码支付的人次；
（3）推广期结束后，车队对乘客的支付方式进行统计，结果如表2
表2：
支付方式 | 现金 | 乘车卡 | 扫码 |
比例 |
|
|
|
已知该线路公交车票价为2元，使用现金支付的乘客无优惠，使用乘车卡支付的乘客享受8折优惠，扫码支付的乘客随机优惠，根据统计结果得知，使用扫码支付的乘客，享受7折优惠的概率为
，享受8折优惠的概率为
，享受9折优惠的概率为
．根据所给数据以事件发生的频率作为相应事件发生的概率，估计一名乘客一次乘车的平均费用．
参考数据：
|
|
|
|
|
66 | 1.54 | 2.711 | 50.12 | 3.47 |
其中
，
