题目内容
设⊙C1,⊙C2,…,⊙Cn是圆心在抛物线y=x2上的一系列圆,它们圆心的横坐标分别记为a1,a2,…,an,已知a1=
,a1>a2>…>an>0,若⊙Ck(k=1,2,3,…,n)都与x轴相切,且顺次两圆外切.
(1)求证:{
}是等差数列;
(2)求an的表达式;
(3)求证:a12+a22+…+an2<
.
| 1 |
| 4 |
(1)求证:{
| 1 |
| an |
(2)求an的表达式;
(3)求证:a12+a22+…+an2<
| 1 |
| 4 |
分析:(1)由题意知:⊙Cn:rn=xn2=an2,⊙Cn-1 ;rn-1=an-12,根据两圆相外切的性质可知|Cn-1Cn|=rn-1+rn,根据两点间的距离公式整理可求
-
=2,根据等差数列的通项公式可求
进而可求an
(2)根据(1)可求
,进而可求an
(3)由
=
•
<
•
=
(
-
),利用裂项求和及不等式的放缩法可证
| 1 |
| an |
| 1 |
| an-1 |
| 1 |
| an |
(2)根据(1)可求
| 1 |
| an |
(3)由
| a | 2 n |
| 1 |
| 4 |
| 1 |
| (n+1)2 |
| 1 |
| 4 |
| 1 |
| n(n+1) |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
解答:(1)证明:由题意知:rn=yn=xn2=an2,rn-1=an-12
所以Cn-1(an-1,an-12),Cn(an,an2)…(2分)
∵|Cn-1Cn|=rn-1+rn,
∴
=an-12+an2…(4分)
两边平方,整理得 (an-1-an)2=4an-12an2…(5分)
∵an-1>an,
∴an-1-an=2an-1an…(6分)
∴
-
=2…(7分)
故{
}是以4为首项,公差为2的等差数列.…(8分)
(2)解:由(1)知,
=4+2(n-1),
∴an=
…(10分)
(3)证明:∵
=
•
<
•
…(11分)
=
(
-
)…(12分)
∴
+
+…+
=
(
-
)=
(1-
)=
-
<
…(14分)
所以Cn-1(an-1,an-12),Cn(an,an2)…(2分)
∵|Cn-1Cn|=rn-1+rn,
∴
| (an-1-an)2+(an-1-an2)2 |
两边平方,整理得 (an-1-an)2=4an-12an2…(5分)
∵an-1>an,
∴an-1-an=2an-1an…(6分)
∴
| 1 |
| an |
| 1 |
| an-1 |
故{
| 1 |
| an |
(2)解:由(1)知,
| 1 |
| an |
∴an=
| 1 |
| 2n+2 |
(3)证明:∵
| a | 2 n |
| 1 |
| 4 |
| 1 |
| (n+1)2 |
| 1 |
| 4 |
| 1 |
| n(n+1) |
=
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
∴
| a | 2 1 |
| a | 2 2 |
| a | 2 n |
=
| n |
 |
| k=1 |
| 1 |
| 4 |
| 1 |
| k |
| 1 |
| k-1 |
| 1 |
| 4 |
| 1 |
| n+1 |
| 1 |
| 4 |
| 1 |
| 4(n+1) |
| 1 |
| 4 |
点评:本题主要考查了圆的外切性质的应用,利用构造等差数列求解数列的通项公式及裂项求和方法的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
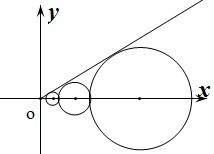
 设C1,C2,…,Cn,…是坐标平面上的一列圆,它们的圆心都在x轴的正半轴上,且都与直线
设C1,C2,…,Cn,…是坐标平面上的一列圆,它们的圆心都在x轴的正半轴上,且都与直线