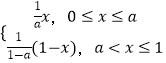题目内容
【题目】已知函数g(x)= ![]() +lnx在[1,+∞)上为增函数,且θ∈(0,π),f(x)=mx﹣
+lnx在[1,+∞)上为增函数,且θ∈(0,π),f(x)=mx﹣ ![]() ﹣lnx(m∈R).
﹣lnx(m∈R).
(Ⅰ)求θ的值;
(Ⅱ)若f(x)﹣g(x)在[1,+∞)上为单调函数,求m的取值范围;
(Ⅲ)设h(x)= ![]() ,若在[1,e]上至少存在一个x0 , 使得f(x0)﹣g(x0)>h(x0)成立,求m的取值范围.
,若在[1,e]上至少存在一个x0 , 使得f(x0)﹣g(x0)>h(x0)成立,求m的取值范围.
【答案】解:(1)由题意, ![]() ≥0在[1,+∞)上恒成立,即
≥0在[1,+∞)上恒成立,即 ![]() .∵θ∈(0,π),∴sinθ>0.故sinθx﹣1≥0在[1,+∞)上恒成立,只须sinθ1﹣1≥0,
.∵θ∈(0,π),∴sinθ>0.故sinθx﹣1≥0在[1,+∞)上恒成立,只须sinθ1﹣1≥0,
即sinθ≥1,只有sinθ=1.结合θ∈(0,π),得 ![]() .
.
2)由(1),得f(x)﹣g(x)= ![]() .
.
∴ ![]() .
.
∵f(x)﹣g(x)在其定义域内为单调函数,
∴mx2﹣2x+m≥0或者mx2﹣2x+m≤0在[1,+∞)恒成立.mx2﹣2x+m≥0等价于m(1+x2)≥2x,即 ![]() ,
,
而 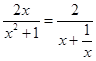 ,(
,( ![]() )max=1,∴m≥1.mx2﹣2x+m≤0等价于m(1+x2)≤2x,即
)max=1,∴m≥1.mx2﹣2x+m≤0等价于m(1+x2)≤2x,即 ![]()
在[1,+∞)恒成立,而 ![]() ∈(0,1],m≤0.
∈(0,1],m≤0.
综上,m的取值范围是(﹣∞,0]∪[1,+∞).
3)构造F(x)=f(x)﹣g(x)﹣h(x), ![]() .
.
当m≤0时,x∈[1,e], ![]() ,
, ![]() ,
,
所以在[1,e]上不存在一个x0 , 使得f(x0)﹣g(x0)>h(x0)成立.
当m>0时, ![]() .
.
因为x∈[1,e],所以2e﹣2x≥0,mx2+m>0,
所以(F(x))'>0在x∈[1,e]恒成立.
故F(x)在[1,e]上单调递增, ![]() ,只要
,只要 ![]() ,
,
解得 ![]() .
.
故m的取值范围是 ![]()
【解析】(1)由题意可知 ![]() .由θ∈(0,π),知sinθ>0.再由sinθ≥1,结合θ∈(0,π),可以得到θ的值.(2)由题设条件知
.由θ∈(0,π),知sinθ>0.再由sinθ≥1,结合θ∈(0,π),可以得到θ的值.(2)由题设条件知 ![]() .mx2﹣2x+m≥0或者mx2﹣2x+m≤0在[1,+∞)恒成立.由此知
.mx2﹣2x+m≥0或者mx2﹣2x+m≤0在[1,+∞)恒成立.由此知 ![]() ,由此可知m的取值范围.(3)构造F(x)=f(x)﹣g(x)﹣h(x),
,由此可知m的取值范围.(3)构造F(x)=f(x)﹣g(x)﹣h(x), ![]() .由此入手可以得到m的取值范围是
.由此入手可以得到m的取值范围是 ![]() .
.
【考点精析】掌握函数单调性的性质和利用导数研究函数的单调性是解答本题的根本,需要知道函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集;一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.