题目内容
(本小题满分8分)已知直线 经过点
经过点 ,且垂直于直线
,且垂直于直线 ,
,
(1)求直线 的方程;(2)求直线
的方程;(2)求直线 与两坐标轴围成三角形的面积。
与两坐标轴围成三角形的面积。
(1)  x-y-2=0. (2)直线l与两坐标轴围成三角形的面积S=
x-y-2=0. (2)直线l与两坐标轴围成三角形的面积S= ·
· ·2=
·2= .
.
解析试题分析:(Ⅰ)联立两直线方程得到方程组,求出方程组的解集即可得到交点P的坐标,根据直线l与x-2y-1垂直,利用两直线垂直时斜率乘积为-1,可设出直线l的方程,把P代入即可得到直线l的方程;
(Ⅱ)分别令x=0和y=0求出直线l与y轴和x轴的截距,然后根据三角形的面积函数间,即可求出直线l与两坐标轴围成的三角形的面积.
考点:本题主要是考查学生会利用联立两直线的方程的方法求两直线的交点坐标,掌握直线的一般式方程,会求直线与坐标轴的截距,是一道中档题.
点评:解决该试题的关键是利用联系方程组的思想得到焦点的坐标,结合垂直关系设出直线方程,进而代点得到结论,同时利用截距来表示边长求解面积。
解:(1) 直线 的斜率为
的斜率为 , …(1分)
, …(1分)
因为直线 垂直于直线
垂直于直线 ,所以
,所以 的斜率为
的斜率为 , …(2分)
, …(2分)
又直线l经过点(0,-2),所以其方程为 x-y-2=0. …(4分)
x-y-2=0. …(4分)
(2)由直线l的方程知它在x轴、y轴上的截距分别是 ,-2, …(6分)
,-2, …(6分)
所以直线l与两坐标轴围成三角形的面积S= ·
· ·2=
·2= . …(8分)
. …(8分)

练习册系列答案
相关题目
 ,求:
,求: 、
、 到直线
到直线 的距离相等,且直线
的距离相等,且直线 和
和 的交点,求直线
的交点,求直线 、
、 ,使
,使 ,
,
 .
.
 的方程为
的方程为 .
.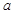 的取值范围.
的取值范围. :
: ,直线
,直线 :
: .若
.若
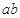 的取值范围.
的取值范围. :
: 和直线
和直线 :
: .
. 的值.
的值.