题目内容
某射手射击所得环数ξ的分布列如下:ξ | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
P | 0.02 | 0.04 | 0.06 | 0.09 | 0.28 | 0.29 | 0.22 |
如果命中8&10环为优秀,那么他射击一次为优秀的概率是( )
A.0.29 B.0.57 C.0.79 D.0.51
分析:一般地,离散型随机变量在某一范围内取值的概率等于它取这个范围内各个值的概率之和.
解:根据射手射击所得环数的分布列,有
P(ξ=8)=0.28,P(ξ=9)=0.29,P(ξ=10)=0.22,
所求概率为P(ξ≥8)=0.28+0.29+0.22=0.79.
答案:C

练习册系列答案
相关题目
 的分布列如下:
的分布列如下: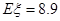 ,则y的值为
.
,则y的值为
.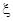 的分布列如下:
的分布列如下: