题目内容
已知圆C:x2+y2+x-6y+m=0与直线l:x+2y-3=0.
(1)若直线l与圆C没有公共点,求m的取值范围;
(2)若直线l与圆C相交于P、Q两点,O为原点,且OP⊥OQ,求实数m的值.
(1)若直线l与圆C没有公共点,求m的取值范围;
(2)若直线l与圆C相交于P、Q两点,O为原点,且OP⊥OQ,求实数m的值.
(1)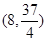 (2)m=3
(2)m=3
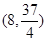 (2)m=3
(2)m=3(1)将圆的方程配方,
得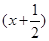 2+(y-3)2=
2+(y-3)2=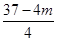 ,
,
故有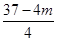 >0,解得m<
>0,解得m<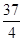 .
.
将直线l的方程与圆C的方程组成方程组,得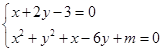
消去y,得x2+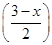 2+x-6×
2+x-6×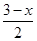 +m=0,
+m=0,
整理,得5x2+10x+4m-27=0, ①
∵直线l与圆C没有公共点,∴方程①无解,故有Δ=102-4×5(4m-27)<0,解得m>8.∴m的取值范围是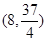 .
.
(2)设P(x1,y1),Q(x2,y2),
由OP⊥OQ,得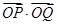 =0,即x1x2+y1y2=0, ②
=0,即x1x2+y1y2=0, ②
由①及根与系数的关系,得
x1+x2=-2,x1·x2=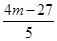 , ③
, ③
又∵P、Q在直线x+2y-3=0上,
∴y1·y2=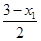 ·
·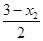 =
= [9-3(x1+x2)+x1·x2],
[9-3(x1+x2)+x1·x2],
将③代入上式,得y1·y2=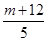 , ④
, ④
将③④代入②得x1·x2+y1·y2=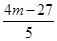 +
+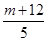 =0,解得m=3.
=0,解得m=3.
代入方程①检验得Δ>0成立,∴m=3.
得
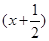 2+(y-3)2=
2+(y-3)2=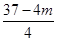 ,
,故有
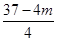 >0,解得m<
>0,解得m<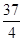 .
.将直线l的方程与圆C的方程组成方程组,得
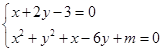
消去y,得x2+
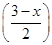 2+x-6×
2+x-6×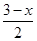 +m=0,
+m=0,整理,得5x2+10x+4m-27=0, ①
∵直线l与圆C没有公共点,∴方程①无解,故有Δ=102-4×5(4m-27)<0,解得m>8.∴m的取值范围是
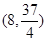 .
.(2)设P(x1,y1),Q(x2,y2),
由OP⊥OQ,得
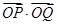 =0,即x1x2+y1y2=0, ②
=0,即x1x2+y1y2=0, ②由①及根与系数的关系,得
x1+x2=-2,x1·x2=
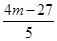 , ③
, ③又∵P、Q在直线x+2y-3=0上,
∴y1·y2=
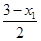 ·
·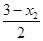 =
= [9-3(x1+x2)+x1·x2],
[9-3(x1+x2)+x1·x2],将③代入上式,得y1·y2=
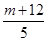 , ④
, ④将③④代入②得x1·x2+y1·y2=
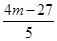 +
+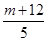 =0,解得m=3.
=0,解得m=3.代入方程①检验得Δ>0成立,∴m=3.

练习册系列答案
相关题目
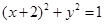 相切,若切点在第二象限,则该直线的方程为 .
相切,若切点在第二象限,则该直线的方程为 .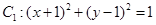 ,圆
,圆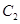 与圆
与圆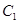 关于直线
关于直线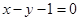 对称,则圆
对称,则圆
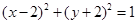


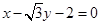 将圆
将圆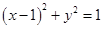 分割成的两段圆孤长之比为( )
分割成的两段圆孤长之比为( )



 过圆
过圆 的圆心,则
的圆心,则 的值为 .
的值为 . :
: 被圆
被圆
 截得的弦
截得的弦 的长是 .
的长是 . 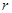 是常数,如果
是常数,如果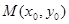 是圆
是圆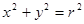 外的一点,那么直线
外的一点,那么直线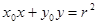 与圆
与圆