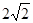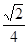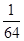题目内容
(本小题满分10分)已知函数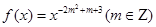 为偶函数,且在
为偶函数,且在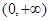 上为增函数.
上为增函数.
(1)求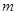 的值,并确定
的值,并确定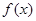 的解析式;
的解析式;
(2)若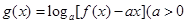 且
且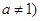 ,是否存在实数
,是否存在实数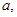 使
使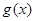 在区间
在区间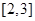 上的最大值为2,若存在,求出
上的最大值为2,若存在,求出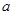 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
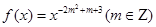 为偶函数,且在
为偶函数,且在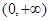 上为增函数.
上为增函数.(1)求
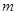 的值,并确定
的值,并确定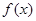 的解析式;
的解析式;(2)若
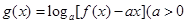 且
且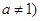 ,是否存在实数
,是否存在实数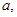 使
使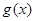 在区间
在区间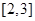 上的最大值为2,若存在,求出
上的最大值为2,若存在,求出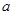 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.(1)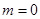 或
或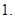 ,
,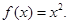
(2) 存在实数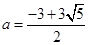 ,使
,使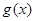 在区间
在区间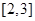 上的最大值为2
上的最大值为2
 或
或 ,
,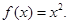
(2) 存在实数
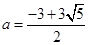 ,使
,使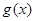 在区间
在区间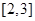 上的最大值为2
上的最大值为2 试题分析:(1)由条件幂函数
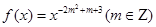 ,在
,在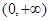 上为增函数,
上为增函数,得到
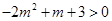
解得
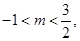 2分
2分又因为
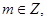
所以
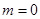 或
或 3分
3分又因为是偶函数
当
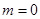 时,
时,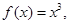 不满足
不满足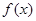 为奇函数;
为奇函数;当
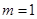 时,
时,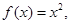 满足
满足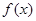 为偶函数;
为偶函数; 所以
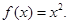 5分
5分(2)
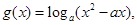 令
令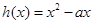 ,
,由
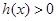 得:
得: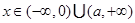
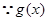 在
在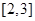 上有定义,
上有定义,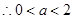 且
且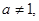
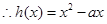 在
在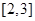 上为增函数. 7分
上为增函数. 7分当
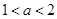 时,
时,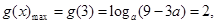
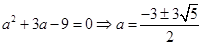
因为
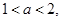 所以
所以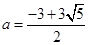 8分
8分当
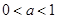 时,
时,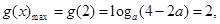
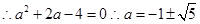
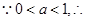 此种情况不存在, 9分
此种情况不存在, 9分综上,存在实数
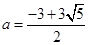 ,使
,使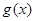 在区间
在区间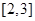 上的最大值为2 10分
上的最大值为2 10分点评:解决该试题的关键是能理解函数的奇偶性和单调性的运用,能理解复合函数的性质得到最值,属于基础题。

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
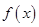 的图像经过点
的图像经过点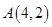 ,则它在A点处的切线的斜率为 .
,则它在A点处的切线的斜率为 .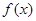 的图像经过
的图像经过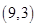 ,则
,则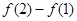 等于( )
等于( )



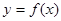 的图象过点
的图象过点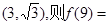 .
.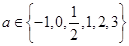 ,则使函数
,则使函数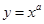 的定义域为R且为奇函数的所有
的定义域为R且为奇函数的所有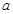 的值有( )
的值有( )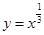 的图像是 ( )
的图像是 ( ) 
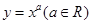 图像经过不等式组
图像经过不等式组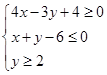 表示的区域,则a的取值范围是
表示的区域,则a的取值范围是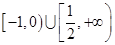


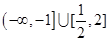
 的图像过点
的图像过点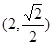 ,则
,则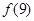 =_______.
=_______.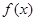 的图象过点(2,
的图象过点(2,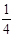 ),则
),则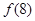 的值是 ( )
的值是 ( )