题目内容
已知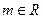 ,命题
,命题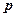 :对任意
:对任意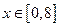 ,不等式
,不等式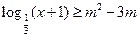 恒成立;命题
恒成立;命题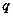 :存在
:存在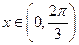 ,使不等式
,使不等式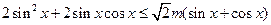 成立.
成立.
(1)若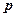 为真命题,求
为真命题,求 的取值范围;
的取值范围;
(2)若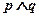 为假,
为假,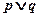 为真,求
为真,求 的取值范围。
的取值范围。
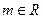 ,命题
,命题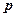 :对任意
:对任意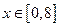 ,不等式
,不等式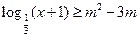 恒成立;命题
恒成立;命题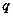 :存在
:存在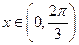 ,使不等式
,使不等式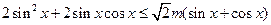 成立.
成立.(1)若
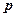 为真命题,求
为真命题,求 的取值范围;
的取值范围;(2)若
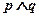 为假,
为假,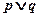 为真,求
为真,求 的取值范围。
的取值范围。解:(1)令
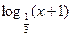 ,
,
则 在
在 上为减函数,
上为减函数,
因为 ,所以当
,所以当 时,
时,
不等式 恒成立,等价于
恒成立,等价于 ,
,
解得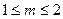 .
.
(Ⅱ)不等式 ,
,
即 ,
,
所以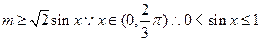 ,
,
即命题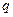 :
: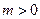 .
.
若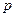 且
且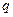 为假,
为假,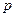 或
或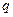 为真,则
为真,则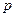 与
与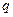 有且只有一个为真.
有且只有一个为真.
若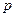 为真,
为真,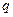 为假,那么
为假,那么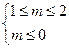 ,则无解;
,则无解;
若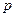 为假,
为假,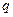 为真,那么
为真,那么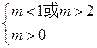 ,则
,则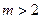 .
.
综上所述,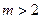

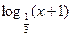 ,
,则
 在
在 上为减函数,
上为减函数,因为
 ,所以当
,所以当 时,
时,
不等式
 恒成立,等价于
恒成立,等价于 ,
,解得
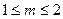 .
.(Ⅱ)不等式
 ,
,即
 ,
,所以
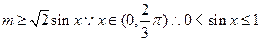 ,
,即命题
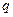 :
: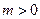 .
. 若
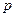 且
且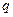 为假,
为假,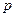 或
或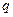 为真,则
为真,则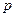 与
与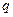 有且只有一个为真.
有且只有一个为真.若
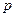 为真,
为真,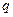 为假,那么
为假,那么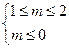 ,则无解;
,则无解;若
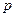 为假,
为假,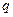 为真,那么
为真,那么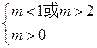 ,则
,则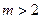 .
.综上所述,
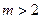
略

练习册系列答案
相关题目
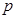 :关于x的函数
:关于x的函数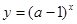 为增函数;命题
为增函数;命题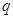 :不等式
:不等式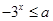 对一切正实数均成立. (1)若命题
对一切正实数均成立. (1)若命题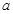 的取值范围;
的取值范围;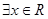 ,使得
,使得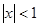 ”的否定是( )
”的否定是( )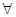 x
x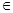 R,都有
R,都有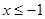 或
或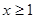
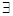 x
x
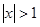
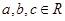 ,命题“若
,命题“若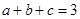 ,则
,则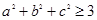 的否命题是
的否命题是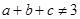 ,则
,则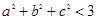
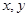 都是奇数,则
都是奇数,则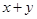 是偶数”,在它的逆命题,否命题,逆否命题中真命题有( )个
是偶数”,在它的逆命题,否命题,逆否命题中真命题有( )个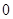
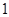
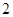
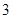
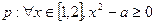 ,命题
,命题
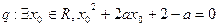 ,
,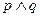 是真命题,求实数a的取值范围.
是真命题,求实数a的取值范围.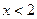 ,则
,则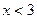 ;
;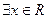 ,
,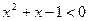 ;
;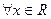 ,
,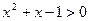 ;
;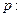 方程
方程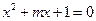 有两个不等的负根;
有两个不等的负根;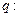 方程
方程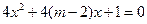 无实根,若
无实根,若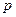 或
或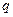 为真,
为真,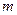 的取值范围。
的取值范围。