题目内容
(本小题满分12分)
若数列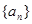 的前
的前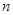 项和
项和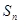 是
是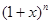 二项展开式中各项系数的和
二项展开式中各项系数的和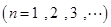 .
.
(Ⅰ)求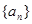 的通项公式;
的通项公式;
(Ⅱ)若数列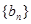 满足
满足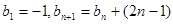 ,且
,且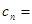
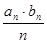 ,求数列
,求数列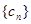 的通项及其前
的通项及其前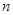 项和
项和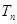 ;
;
(III)求证: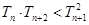 .
.
【答案】
(Ⅰ)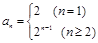
(Ⅱ)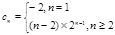 ,
,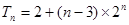
(III)证明见解析
【解析】(Ⅰ)由题意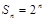 ,
, 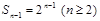 ,两式相减得
,两式相减得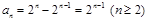 .3分
.3分
当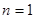 时,
时,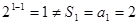 ,∴
,∴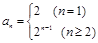 .
-------4分
.
-------4分
(Ⅱ)∵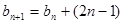 ,∴
,∴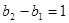 ,
, 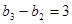 ,
,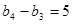 ,………
,………
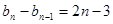 .以上各式相加得
.以上各式相加得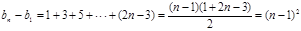 .
.
∵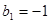 ,∴
,∴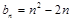 . --- -6分∴
. --- -6分∴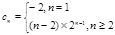 .
-----7分
.
-----7分
∴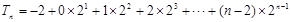 ,
,
∴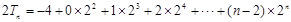 .
.
∴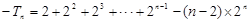 .
. 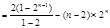
= .
∴
.
∴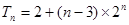 . ----------9分
. ----------9分
(3)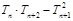 =
=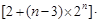
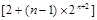
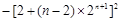
=4+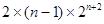
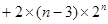
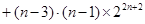
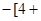
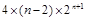
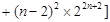 =
=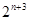
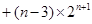
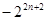
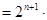
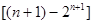 .
∵
.
∵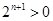 , ∴ 需证明
, ∴ 需证明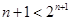 ,用数学归纳法证明如下:
,用数学归纳法证明如下:
①当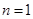 时,
时,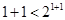 成立
②假设
成立
②假设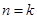 时,命题成立即
时,命题成立即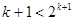 ,
,
那么,当 时,
时,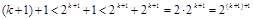 成立.
成立.
由①、②可得,对于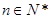 都有
都有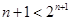 成立.
成立.
∴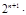
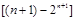
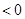 . ∴
. ∴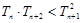 .---12分
.---12分

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目