Question

（2012•黔东南州一模）在集合A={（x，y）|x≥1，y≥1，x+y≤4}中，x+2y的最大值是（　　）

A．5

B．6

C．7

D．8

Answer 1

分析：本题只要作出可行域，记目标函数z=x+2y，直线的斜率为-

1

2

，截距为

z

2

，先作出直线y=-

x

2

，平移过程发现，直线过点A（1，3）时，截距

z

2

取最大值，即z取最大值为7．

解答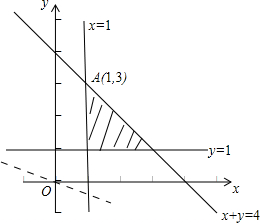：解：集合A对应的平面区域如图所示的阴影部分，记z=x+2y，可得y=-

x

2

+

z

2

，
故直线的斜率为-

1

2

，截距为

z

2

，先作出一条斜率为-

1

2

的直线y=-

x

2

（图中的虚线），
当直线平移到经过点A（1，3）时，截距

z

2

取最大值，即z取最大值为1+2×3=7，
故选C．

点评：本题为线性规划问题，关键正确是作出可行域，再平移直线可得取最值时经过的点，只要把坐标代到目标函数即可，数中档题．