题目内容
10．已知复数z满足（3-4i）z=25，则z对应的点位于复平面的（ ）| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
分析 求出复数z，得到对应点的坐标即可判断选项．
解答 解：复数z满足（3-4i）z=25，
可得z=$\frac{25}{3-4i}$=$\frac{25（3+4i）}{（3-4i）（3+4i）}$=3+4i．对应点为：（3，4），在第一象限．
故选：A．
点评 本题考查复数的代数形式的混合运算，复数的几何意义，是基础题．
练习册系列答案
相关题目
20．己知程序框图如图所示，执行相应程序，若输出S=15，则框图中①处可以填入（ ）
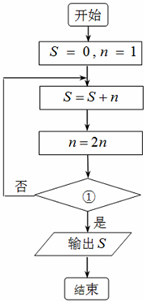
| A． | n≥4？ | B． | n＞8？ | C． | n＞4？ | D． | n≥8？ |
5．对某种灯泡中随机地抽取200个样品进行使用寿命调查，结果如下：
规定：使用寿命大于或等于500天的灯泡是优等品，小于300天是次品，其余的是正品．某人从灯泡样品中随机地购买了n（n∈N*）个，如果这n个灯泡的等级分布情况恰好与从这200个样品中按三个等级分层抽样所得的结果相同，则n的最小值为（ ）
| 寿命（天） | 频数 | 频率 |
| [100，200） | 20 | 0.10 |
| [200，300） | 30 | y |
| [300，400） | 70 | 0.35 |
| [400，500） | x | 0.15 |
| [500，600） | 50 | 0.25 |
| 合计 | 200 | 1 |
| A． | 2 | B． | 3 | C． | 4 | D． | 5 |
2．已知a＞0且a≠1，则使关于x的方程loga（x-2ak）=loga（x2-a2）有解的k的取值范围是（ ）
| A． | 0＜k＜$\frac{1}{2}$或k$＜-\frac{1}{2}$ | B． | 0＜k＜1或k＜-1 | C． | 0＜k＜2或k＜-2 | D． | 0＜k＜1或k＜-2 |
20．函数y=f（x）（x∈（0，3））图象如图所示，若0＜x1＜x2＜3，则有（ ）
| A． | $\frac{f（{x}_{1}）}{{x}_{1}}$＜$\frac{f（{x}_{2}）}{{x}_{2}}$ | B． | $\frac{f（{x}_{1}）}{{x}_{1}}$=$\frac{f（{x}_{2}）}{{x}_{2}}$ | ||
| C． | $\frac{f（{x}_{1}）}{{x}_{1}}$＞$\frac{f（{x}_{2}）}{{x}_{2}}$ | D． | 前三个判断都不正确 |