题目内容
3．设Sn是等差数列{an}的前n项和，若a1：a2=1：2，则S1：S3=（ ）| A． | 1：3 | B． | 1：4 | C． | 1：5 | D． | 1：6 |
分析 由题意易得d=a1，进而可得S3=6a1，易得要求的比值．
解答 解：设等差数列{an}的公差为d，
∵a1：a2=1：2，∴a1：（a1+d）=1：2，
解得d=a1，∴S3=3a1+$\frac{3×2}{2}$d=6a1，
∴S1：S3=a1：（6a1）=1：6
故选：D
点评 本题考查等差数列的求和公式，属基础题．
练习册系列答案
相关题目
13．
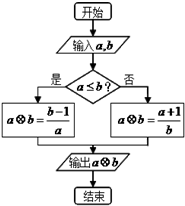对任意非零实数a，b，定义a⊕b的算法原理如右侧程序框图所示．设a=$\frac{5}{2}$，b=2，则计算机执行该运算后输出的结果是（ ）
对任意非零实数a，b，定义a⊕b的算法原理如右侧程序框图所示．设a=$\frac{5}{2}$，b=2，则计算机执行该运算后输出的结果是（ ）| A． | $\frac{7}{5}$ | B． | $\frac{7}{4}$ | C． | $\frac{7}{3}$ | D． | $\frac{7}{2}$ |
18．设△ABC的外接圆的圆心为P，半径为3，若$\overrightarrow{PA}$$+\overrightarrow{PB}$=$\overrightarrow{CP}$，则$\overrightarrow{PA}•\overrightarrow{PB}$=（ ）
| A． | -$\frac{9}{2}$ | B． | -$\frac{3}{2}$ | C． | 3 | D． | 9 |
15．在[0，2π]上，满足sinx≥$\frac{\sqrt{3}}{2}$的x的取值范围是（ ）
| A． | [0，$\frac{π}{3}$] | B． | [$\frac{π}{3}$，$\frac{5π}{3}$] | C． | [$\frac{π}{3}$，$\frac{2π}{3}$] | D． | [$\frac{5π}{6}$，π] |
13．在等差数列{an}中，a7=8，前7项和S7=42，则其公差是（ ）
| A． | -$\frac{1}{3}$ | B． | $\frac{1}{3}$ | C． | -$\frac{2}{3}$ | D． | $\frac{2}{3}$ |