题目内容
一船自西向东匀速航行上午10时到达一座灯塔P的南偏西75°距塔68海里的M处,下午2时到达这座灯塔的东南方向的N处,则这只船航行的速度为( )
A.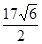 海里/小时 海里/小时 | B.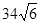 海里/小时 海里/小时 |
C. 海里/小时 海里/小时 | D.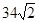 海里/小时 海里/小时 |
A
解析试题分析:在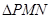 中,
中,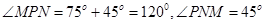 ,由正弦定理,
,由正弦定理,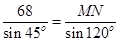 ,因此
,因此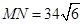 ,因此航行速度为
,因此航行速度为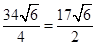 .
.
考点:1、方位角;2、正弦定理解三角形.

练习册系列答案
相关题目
设锐角 的三内角
的三内角 、
、 、
、 所对边的边长分别为
所对边的边长分别为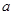 、
、 、
、 ,且
,且 ,
, ,则
,则 的取值范围为( ).
的取值范围为( ).
A. | B. | C. | D. |
在 中,若
中,若 ,则
,则 的形状一定是
的形状一定是
| A.等边三角形 | B.不含 角的等腰三角形 角的等腰三角形 |
| C.钝角三角形 | D.直角三角形 |
在三角形 中,角
中,角 对应的边分别为
对应的边分别为 ,若
,若 ,
, ,
, ,则
,则 =( )
=( )
A. | B. | C. | D. |
在 中,内角
中,内角 的对边分别是
的对边分别是 若
若 ,则
,则 =( )
=( )
A. | B. | C. | D.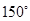 |
在△ABC中,∠A=60°,AB=2,且△ABC的面积为 ,则BC的长为( ).
,则BC的长为( ).
A. | B.3 | C. | D.7 |
 ,则A等于( )
,则A等于( ) 且∠ABC=60°,AB=2,BC=4,则球O的表面积为( )
且∠ABC=60°,AB=2,BC=4,则球O的表面积为( ) B.
B. C.
C. D.
D.
 中,角A、B、C的对边分别为
中,角A、B、C的对边分别为 、
、 、
、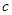 ,已知
,已知 ,
, B.
B. C.
C. D.
D.