题目内容
在等差数列 中,已知
中,已知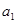 +
+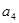 +
+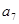 =39,
=39, +
+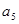 +
+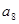 =33,则
=33,则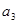 +
+ +
+ =( )
=( )
| A.30 | B.27 | C.24 | D.21 |
B
解析试题分析:因为根据已知条件,等差数列 中,已知
中,已知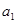 +
+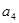 +
+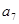 =39,
=39, +
+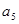 +
+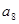 =33,根据三项整体的相差为3个公差,得到
=33,根据三项整体的相差为3个公差,得到 +
+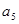 +
+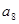 -(
-(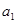 +
+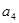 +
+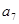 )=3d=-6,d=-2,则
)=3d=-6,d=-2,则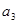 +
+ +
+ =(
=( +
+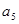 +
+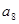 )+3d=33-6=27,故选B.
)+3d=33-6=27,故选B.
考点:等差数列
点评:等差数列的求和的运用,主要是整体思想,是解决的关键,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知等差数列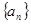 的公差为2,若
的公差为2,若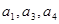 成等比数列, 则
成等比数列, 则 =( )
=( )
A.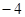 | B.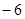 | C.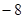 | D.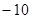 |
已知等差数列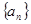 的公差为
的公差为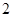 ,若
,若 成等比数列, 则
成等比数列, 则 ( )
( )
A.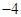 | B.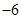 | C.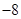 | D.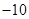 |
设等差数列 的前n项和为
的前n项和为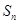 ,若
,若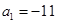 ,
, ,则当
,则当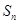 取最小值时,n等于( )
取最小值时,n等于( )
| A.6 | B.7 | C.8 | D.9 |
数列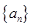 的首项为
的首项为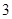 ,
,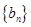 为等差数列且
为等差数列且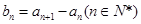 .若则
.若则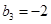 ,
,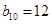 ,则
,则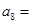 ( )
( )
| A.0 | B.3 | C.8 | D.11 |
已知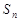 是等差数列
是等差数列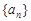 的前
的前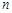 项和,若
项和,若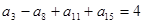 ,则
,则 的值是
的值是
| A.5 | B.8 | C.16 | D.20 |
在等差数列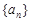 中,已知
中,已知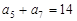 ,则该数列前11项和
,则该数列前11项和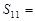
| A.196 | B.132 | C.88 | D.77 |
设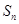 是等差数列{an}的前n项和,
是等差数列{an}的前n项和,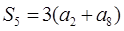 ,则
,则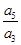 的值为( )
的值为( )
A.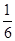 | B.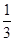 | C.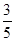 | D.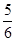 |