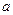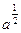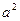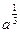题目内容
(本小题满分14分)
已知函数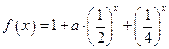 ;
; .
.
(1)当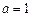 时,求函数f(x)在
时,求函数f(x)在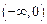 上的值域;
上的值域;
(2)若对任意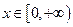 ,总有
,总有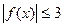 成立,求实数
成立,求实数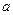 的取值范围;
的取值范围;
(3)若 (
( 为常数),且对任意
为常数),且对任意 ,总有
,总有 成立,求M的取值范围.
成立,求M的取值范围.
已知函数
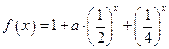 ;
; .
. (1)当
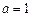 时,求函数f(x)在
时,求函数f(x)在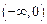 上的值域;
上的值域;(2)若对任意
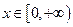 ,总有
,总有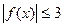 成立,求实数
成立,求实数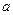 的取值范围;
的取值范围;(3)若
 (
( 为常数),且对任意
为常数),且对任意 ,总有
,总有 成立,求M的取值范围.
成立,求M的取值范围.(1)f(x)在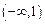 的值域为
的值域为
(2)实数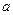 的取值范围为
的取值范围为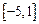
(3)当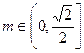 时,M的取值范围是
时,M的取值范围是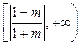 ;
;
当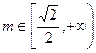 时,M的取值范围是
时,M的取值范围是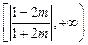
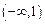 的值域为
的值域为
(2)实数
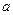 的取值范围为
的取值范围为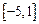
(3)当
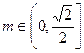 时,M的取值范围是
时,M的取值范围是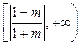 ;
;当
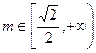 时,M的取值范围是
时,M的取值范围是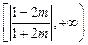
解:(1)当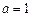 时,
时,
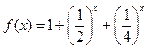 -因为f(x)在
-因为f(x)在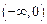 上递减,-----------------2分
上递减,-----------------2分
所以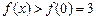 ,即f(x)在
,即f(x)在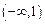 的值域为
的值域为 ----------------4分
----------------4分
(法二)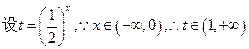 ,
,
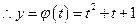 ,对称轴
,对称轴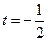 ,
,
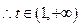 时为增函数,---------------2分
时为增函数,---------------2分
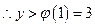 ,f(x)在
,f(x)在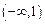 的值域为
的值域为 ------------------4分
------------------4分
(2)由题意知,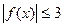 在
在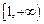 上恒成立。
上恒成立。
 ,
,
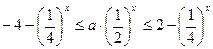
∴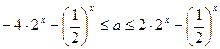 在
在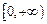 上恒成立
上恒成立
∴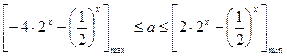 -----------------------------5分
-----------------------------5分
设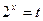 ,
,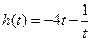 ,
,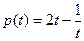 ,由
,由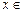
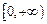 得 t≥1,
得 t≥1,
设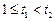 ,
,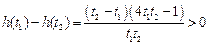 ,
,
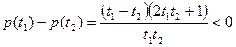
(可用导数方法证明单调性: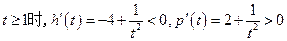 )
)
所以 在
在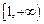 上递减,
上递减, 在
在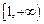 上递增,-------------------------------7分
上递增,-------------------------------7分
 在
在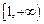 上的最大值为
上的最大值为 ,
,
 在
在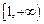 上的最小值为
上的最小值为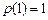
所以实数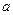 的取值范围为
的取值范围为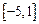 ------------------------------------9分
------------------------------------9分
(3) ,
,
∵ m>0 ,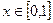
∴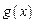 在
在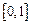 上递减,--------------------------10分
上递减,--------------------------10分
∴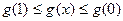
即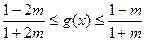 ----------------------------------------11分
----------------------------------------11分
①当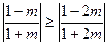 ,即
,即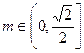 时,
时,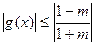 ,
,
此时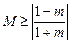 ,-----------------------------------------------------------12分
,-----------------------------------------------------------12分
②当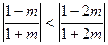 ,即
,即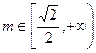 时,
时,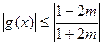 ,
,
此时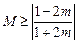 ,---------------------------------------------------------13分
,---------------------------------------------------------13分
综上所述,当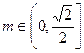 时,M的取值范围是
时,M的取值范围是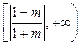 ;
;
当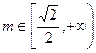 时,M的取值范围是
时,M的取值范围是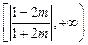 -----------------------------14分
-----------------------------14分
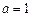 时,
时,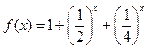 -因为f(x)在
-因为f(x)在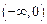 上递减,-----------------2分
上递减,-----------------2分所以
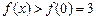 ,即f(x)在
,即f(x)在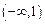 的值域为
的值域为 ----------------4分
----------------4分(法二)
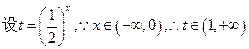 ,
,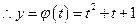 ,对称轴
,对称轴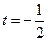 ,
,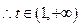 时为增函数,---------------2分
时为增函数,---------------2分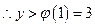 ,f(x)在
,f(x)在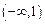 的值域为
的值域为 ------------------4分
------------------4分(2)由题意知,
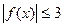 在
在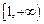 上恒成立。
上恒成立。 ,
, 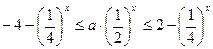
∴
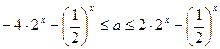 在
在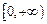 上恒成立
上恒成立∴
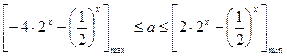 -----------------------------5分
-----------------------------5分设
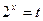 ,
,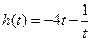 ,
,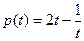 ,由
,由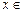
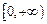 得 t≥1,
得 t≥1,设
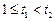 ,
,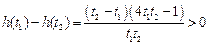 ,
,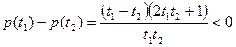
(可用导数方法证明单调性:
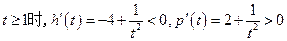 )
)所以
 在
在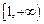 上递减,
上递减, 在
在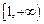 上递增,-------------------------------7分
上递增,-------------------------------7分 在
在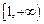 上的最大值为
上的最大值为 ,
,  在
在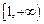 上的最小值为
上的最小值为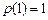
所以实数
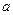 的取值范围为
的取值范围为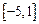 ------------------------------------9分
------------------------------------9分(3)
 ,
,∵ m>0 ,
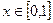
∴
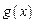 在
在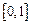 上递减,--------------------------10分
上递减,--------------------------10分∴
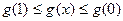
即
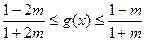 ----------------------------------------11分
----------------------------------------11分①当
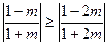 ,即
,即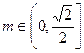 时,
时,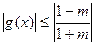 ,
,此时
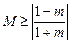 ,-----------------------------------------------------------12分
,-----------------------------------------------------------12分②当
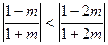 ,即
,即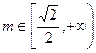 时,
时,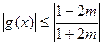 ,
,此时
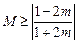 ,---------------------------------------------------------13分
,---------------------------------------------------------13分综上所述,当
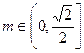 时,M的取值范围是
时,M的取值范围是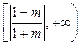 ;
;当
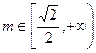 时,M的取值范围是
时,M的取值范围是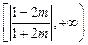 -----------------------------14分
-----------------------------14分
练习册系列答案
相关题目
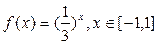 ,函数
,函数
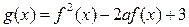 的最小值为
的最小值为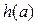 。
。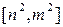
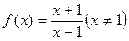 .
. 在
在 上是减函数;
上是减函数; 时,求
时,求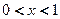 时,则下列大小关系正确的( )
时,则下列大小关系正确的( )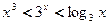 (
(
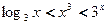 (
(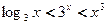
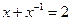 ,则
,则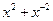 的值为( )
的值为( )

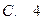

 ,若对任意
,若对任意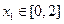 ,存在
,存在 ,使得
,使得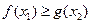 ,则实数
,则实数 的取值范围是 ( )
的取值范围是 ( )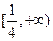
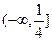
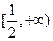
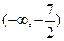
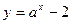 (
(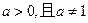 )的图象过点
)的图象过点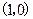 ,那么
,那么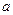 的值等于:
的值等于: 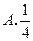
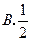
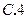
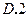 高#
高# 考#资#源#
考#资#源#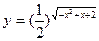 得单调递增区间是 ( )
得单调递增区间是 ( )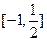
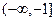
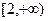
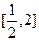
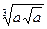 的结果是( )
的结果是( )