题目内容
【题目】椭圆C： 
=1（a＞b＞0）的中心在原点，焦点在x轴上，焦距为2，且与椭圆x2+ 
=1有相同离心率，直线l：y=kx+m与椭圆C交于不同的A，B两点．
（Ⅰ）求椭圆C的方程；
（Ⅱ）若在椭圆C上存在点Q，满足 
，（O为坐标原点），求实数λ取值范围．
【答案】解：（ I）由已知可 
解得 
，∴b=1．
所求椭圆C的方程 
．
（ II）由 
得（1+2k2）x2+4kmx+2m2﹣2=0，
∴△=16k2m2﹣4（1+2k2）（2m2﹣2）=8（1+2k2﹣m2）．
由直线直线l与椭圆C交于不同的A，B两点，有△＞0，∴1+2k2＞m2 ． ①
设点A（x1 ， y1），B（x2 ， y2），则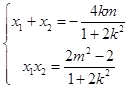 
于是 
．
当m=0时，易知点A，B关于原点对称，则λ=0；
当m≠0时，易知点A，B不关于原点对称，则λ≠0．
由 
，得 
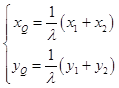即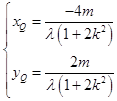 
．
∵Q点在椭圆上，∴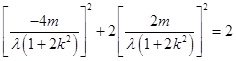 
．
化简得4m2（1+2k2）=λ2（1+2k2）2 ．
∵1+2k2≠0，∴4m2=λ2（1+2k2）． ②
由①②两式可得λ2＜4，∴﹣2＜λ＜2且λ≠0．
综上可得实数λ的取值范围是﹣2＜λ＜2
【解析】（Ⅰ）利用已知条件列出椭圆几何量的方程组，求解a，b，即可求椭圆C的方程；（Ⅱ）联立直线与椭圆方程，利用韦达定理，结合向量关系，推出结果即可．
【考点精析】解答此题的关键在于理解椭圆的标准方程的相关知识，掌握椭圆标准方程焦点在x轴：
，焦点在y轴：
．
练习册系列答案
相关题目
