题目内容
已知向量
=(cosα,sinα),
=(cosβ,sinβ)且|
+
|=
|
-k
|,k>-
,k∈R
(1)用k表示
•
;
(2)当
•
最小时,求向量
+
与向量
-k
的夹角θ.
| a |
| b |
| a |
| b |
| 3 |
| a |
| b |
| 1 |
| 3 |
(1)用k表示
| a |
| b |
(2)当
| a |
| b |
| a |
| b |
| a |
| b |
(1)∵|
+
|2=3|
-k
|2,
∴(cosα+cosβ)2+(sinα+sinβ)2=3[(cosα+kcosβ)2+(sinα+ksinβ)2]
得cos(α-β)=
…(4分)
由k>-
及|cos(α-β)|≤1,
得1-
≤k≤1+
,
∴
•
=cosαcosβ+sinαsinβ=cos(α-β)
=
,k∈[1-
,1+
]…(6分)
令3k+1=t,
则t>0,
k=
(t-1)代入上式可得
•
=
=
(t+
-2)≥
(2
-2)=
当且仅当t=2,
即k=
(t-1)时,
取“=”,(
•
)min=
…(10分)
(2)当
•
最小时,
cosθ=
=
=
…(12分)
将
2=1,
| a |
| b |
| a |
| b |
∴(cosα+cosβ)2+(sinα+sinβ)2=3[(cosα+kcosβ)2+(sinα+ksinβ)2]
得cos(α-β)=
| 1 |
| 2 |
| 3k2+1 |
| 3k+1 |
由k>-
| 1 |
| 3 |
得1-
2
| ||
| 3 |
2
| ||
| 3 |
∴
| a |
| b |
=
| 1 |
| 2 |
| 3k2+1 |
| 3k+1 |
2
| ||
| 3 |
2
| ||
| 3 |
令3k+1=t,
则t>0,
k=
| 1 |
| 3 |
| a |
| b |
| 1 |
| 6 |
| t2-2t+4 |
| t |
| 1 |
| 6 |
| 4 |
| t |
| 1 |
| 6 |
| 4 |
| 1 |
| 3 |
当且仅当t=2,
即k=
| 1 |
| 3 |
取“=”,(
| a |
| b |
| 1 |
| 3 |
(2)当
| a |
| b |
cosθ=
(
| ||||||||
|
|
(
| ||||||||||||||
|
=
| ||||||||||||||||||||||||
|
将
| a |

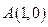 ,
, ,
, ,
,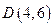 为顶点的四边形是一个矩形.
为顶点的四边形是一个矩形. 的方程
的方程 ,直线
,直线

 的取值范围; (2)若圆
的取值范围; (2)若圆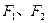 为椭圆
为椭圆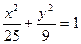 的两个焦点,过
的两个焦点,过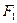 的直线交椭圆于A、B两点若
的直线交椭圆于A、B两点若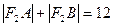 ,则
,则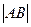 =______
=______