题目内容
由数字1、2、3、4、5、6组成无重复数字的数中,求:
(1)六位偶数的个数;
(2)求三个偶数互不相邻的六位数的个数;
(3)求恰有两个偶数相邻的六位数的个数;
(4)奇数字从左到右,从小到大依次排列的六位数的个数.
(1)六位偶数的个数;
(2)求三个偶数互不相邻的六位数的个数;
(3)求恰有两个偶数相邻的六位数的个数;
(4)奇数字从左到右,从小到大依次排列的六位数的个数.
(1)360,(2)144,(3)432,(4)120.
试题分析:(1)根据排列组合中特殊元素、特殊位置优先考虑的原则,先考虑个位数. 偶数的个位数字必须是偶数,有3种选择,剩下5个元素进行全排列,有
 种排法,根据分步计数原理得满足条件的六位偶数共有
种排法,根据分步计数原理得满足条件的六位偶数共有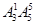 =360个,(2)不相邻问题用插空法解决,先排奇数,有
=360个,(2)不相邻问题用插空法解决,先排奇数,有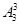 种排法,产生4个空,从四个空选三,排偶数,有
种排法,产生4个空,从四个空选三,排偶数,有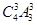 ,根据分步计数原理得满足条件的三个偶数互不相邻的六位数有
,根据分步计数原理得满足条件的三个偶数互不相邻的六位数有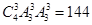 个,(3)相邻问题用捆绑法解决,先从三个偶数中选出两个捆绑在一起看作一个偶数,有
个,(3)相邻问题用捆绑法解决,先从三个偶数中选出两个捆绑在一起看作一个偶数,有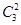 种选法,因为与第三个偶数不相邻,因此进行不相邻排列:先排奇数再从四个空里选两个空插这两个元素,根据分步计数原理得满足条件的恰有两个偶数相邻的六位数共有
种选法,因为与第三个偶数不相邻,因此进行不相邻排列:先排奇数再从四个空里选两个空插这两个元素,根据分步计数原理得满足条件的恰有两个偶数相邻的六位数共有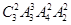 =432个,不要忘记两个捆绑的偶数也要全排列.(4)有序排列,只需选不需排,即从6个位置中选3个填奇数,再排偶数,即
=432个,不要忘记两个捆绑的偶数也要全排列.(4)有序排列,只需选不需排,即从6个位置中选3个填奇数,再排偶数,即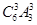 =120个.或用除法,除去顺序数,即
=120个.或用除法,除去顺序数,即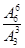 =120个.
=120个.(1)偶数的个位数字必须是偶数。因而先排个位
满足条件的六位偶数共有
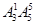 =360个; 3分
=360个; 3分(2)先排奇数,然后有三个空,再插空排三个偶数
满足条件的三个偶数互不相邻的六位数有
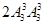 =72个; 6分
=72个; 6分(3)用捆绑法。先从三个偶数中选出两个捆绑在一起看作一个偶数,然后排奇数,
再从四个空里选两个空插这两个元素。满足条件的恰有两个偶数相邻的六位
数共有
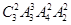 =432个; 10分
=432个; 10分(4)满足条件的奇数字从左到右从小到大依次排列的六位数共有
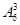 =120个 15分
=120个 15分
练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
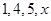 四个不同数字组成四位数,所有这些四位数中的数字的总和为
四个不同数字组成四位数,所有这些四位数中的数字的总和为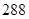 ,则
,则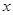 = 。
= 。