题目内容
同时满足以下三个条件的函数是( )
①图像过点 ;②在区间
;②在区间 上单调递减③是偶函数 .
上单调递减③是偶函数 .
A. | B. |
C.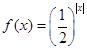 | D.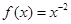 |
C
解析试题分析:选项A中,函数对称轴为x=-1,所以不是偶函数,排除A;
选项B中,函数 在区间
在区间 上单调递增,排除B;
上单调递增,排除B;
选项D中,函数图像不过点 ,排除D.故选择C.
,排除D.故选择C.
考点:函数的图像和性质.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
规定 ,则函数
,则函数 的值域为
的值域为
A. | B. | C. | D. |
若函数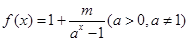 是奇函数,则
是奇函数,则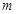 为
为
A.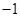 | B.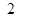 | C.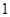 | D.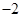 |
函数 的定义域是( )
的定义域是( )
A. | B. | C. | D. |
下列函数中,既是偶函数又在 上单调递增的是 ( )
上单调递增的是 ( )
A. | B. | C. | D. |
已知函数 的定义域为
的定义域为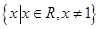 ,且
,且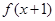 为奇函数,当
为奇函数,当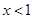 时,
时,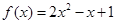 ,那么当
,那么当 时,
时, 的递减区间是( )
的递减区间是( )
A.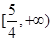 | B. | C.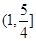 | D.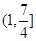 |
已知函数 为奇函数,且当
为奇函数,且当 时,
时, ,则
,则 ( )
( )
A. | B. | C. | D. |
已定义在 上的偶函数
上的偶函数 满足
满足 时,
时, 成立,若
成立,若 ,
, ,
, ,则
,则 的大小关系是( )
的大小关系是( )
A. | B. | C. | D. |
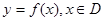 (定义域),若存在常数C,对于任意
(定义域),若存在常数C,对于任意 ,存在唯一的
,存在唯一的 ,使得
,使得 ,则称函数
,则称函数 在D上的“均值”为C.已知函数
在D上的“均值”为C.已知函数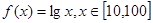 ,则函数
,则函数 上的均值为 ( )
上的均值为 ( ) (B)
(B) (C)10 (D)
(C)10 (D)