题目内容
(本小题满分14分)已知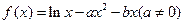 .
.
(1)若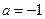 ,函数
,函数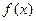 在其定义域内是增函数,求
在其定义域内是增函数,求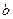 的取值范围.
的取值范围.
(2)在(1)的结论下,设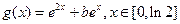 ,求函数
,求函数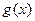 的最小值;
的最小值;
(3)若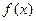 的图象与
的图象与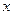 轴交于
轴交于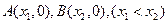 ,
,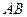 中点为
中点为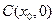 ,求证:
,求证: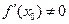 .
.
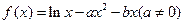 .
.(1)若
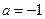 ,函数
,函数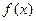 在其定义域内是增函数,求
在其定义域内是增函数,求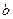 的取值范围.
的取值范围.(2)在(1)的结论下,设
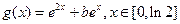 ,求函数
,求函数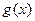 的最小值;
的最小值;(3)若
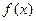 的图象与
的图象与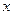 轴交于
轴交于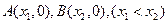 ,
,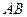 中点为
中点为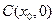 ,求证:
,求证: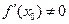 .
.(1)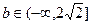 (2)同解析(3)同解析
(2)同解析(3)同解析
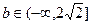 (2)同解析(3)同解析
(2)同解析(3)同解析(1)依题意: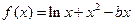
∵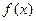 在
在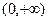 递增
递增
∴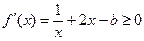 对
对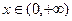 恒成立 ………………1分
恒成立 ………………1分
∴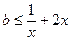 …………………2分
…………………2分
∵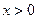
∴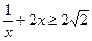 ………………3分
………………3分
当且仅当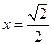 时取“
时取“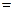 ”,
”,
∴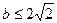 , …………………4分
, …………………4分
且当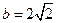 时,
时,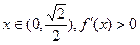 ,
,
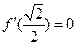 ,
,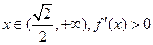
∴符合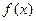 在
在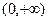 是增函数
是增函数
∴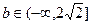
(2)设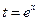 ,∵
,∵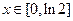
∴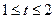 , 则函数
, 则函数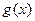 化为:
化为:
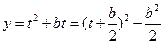 ,
,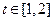 …………………6分
…………………6分
当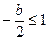 时,即
时,即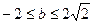 时.
时.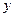 在
在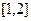 递增
递增
∴当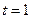 时,
时,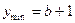
②当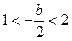 时,即
时,即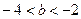 ,当
,当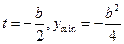
③当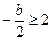 ,即
,即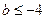 时,
时,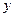 在
在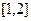 递减,当
递减,当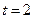 时,
时,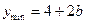
综上: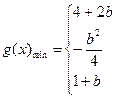
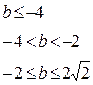 …………………9分
…………………9分
(3)依题意: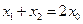 ,假设结论不成立,
,假设结论不成立,
 则有
则有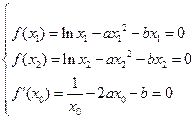 ……………②
……………②
由①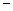 ②得:
②得: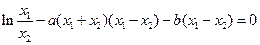 ④ ………………10分
④ ………………10分
由③知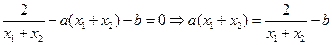 代入④
代入④
得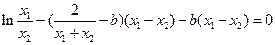
∴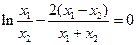 即
即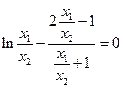 …………………11分
…………………11分
令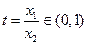 则
则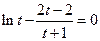 …………⑤ ……………………12分
…………⑤ ……………………12分
令
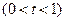
∵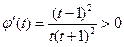 ∴
∴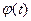 在
在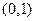 递增 …………………13分
递增 …………………13分
∴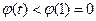 即
即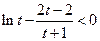
与⑤式矛盾
∴假设不成立
∴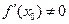 ………………………14分
………………………14分
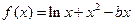
∵
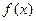 在
在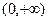 递增
递增 ∴
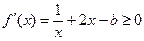 对
对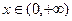 恒成立 ………………1分
恒成立 ………………1分∴
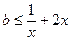 …………………2分
…………………2分∵
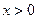
∴
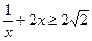 ………………3分
………………3分当且仅当
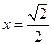 时取“
时取“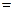 ”,
”,∴
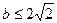 , …………………4分
, …………………4分且当
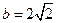 时,
时,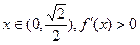 ,
,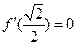 ,
,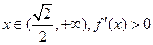
∴符合
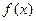 在
在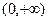 是增函数
是增函数∴
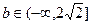
(2)设
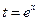 ,∵
,∵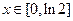
∴
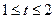 , 则函数
, 则函数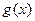 化为:
化为: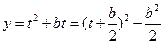 ,
,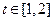 …………………6分
…………………6分当
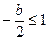 时,即
时,即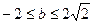 时.
时.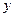 在
在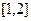 递增
递增∴当
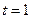 时,
时,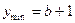
②当
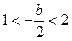 时,即
时,即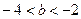 ,当
,当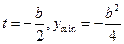
③当
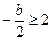 ,即
,即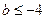 时,
时,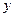 在
在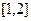 递减,当
递减,当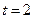 时,
时,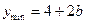
综上:
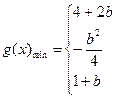
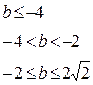 …………………9分
…………………9分(3)依题意:
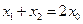 ,假设结论不成立,
,假设结论不成立, 则有
则有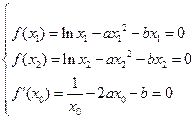 ……………②
……………②由①
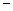 ②得:
②得: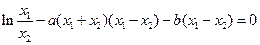 ④ ………………10分
④ ………………10分由③知
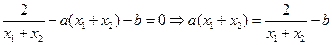 代入④
代入④得
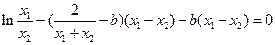
∴
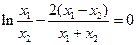 即
即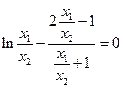 …………………11分
…………………11分令
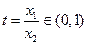 则
则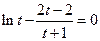 …………⑤ ……………………12分
…………⑤ ……………………12分令

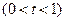
∵
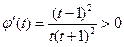 ∴
∴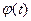 在
在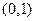 递增 …………………13分
递增 …………………13分∴
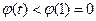 即
即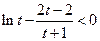
与⑤式矛盾
∴假设不成立
∴
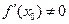 ………………………14分
………………………14分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
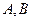 两地的距离是120km.假设汽油的价格是6元/升,以
两地的距离是120km.假设汽油的价格是6元/升,以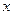 km/h(其中
km/h(其中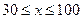 )速度行驶时,汽车的耗油率为
)速度行驶时,汽车的耗油率为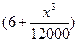 L/h,司机每小时的工资是28元.那么最经济的车速是多少?如不考虑其他费用,这次行车的总费用是多少?
L/h,司机每小时的工资是28元.那么最经济的车速是多少?如不考虑其他费用,这次行车的总费用是多少?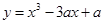 在
在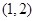 内有极小值,则实数
内有极小值,则实数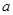 的取值范围是( )
的取值范围是( )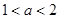
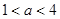
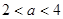

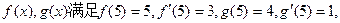 则函数
则函数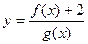 的图像在
的图像在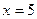 处的切线与坐标轴围成的三角形的面积是 。
处的切线与坐标轴围成的三角形的面积是 。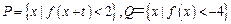 ,
, 的充分不必要条件,则实数
的充分不必要条件,则实数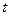 的取值范围是 .
的取值范围是 .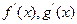 分别是f(x)、g(x)的导函数,且
分别是f(x)、g(x)的导函数,且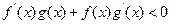 ,则当
,则当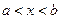 时,有( )
时,有( ) g(a)
g(a)
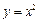 在点(1,1)处的切线的斜率为 .
在点(1,1)处的切线的斜率为 .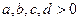 ,且不等于1,
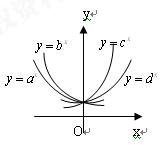
,且不等于1,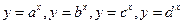 在同一坐标系中的图象如图,则
在同一坐标系中的图象如图,则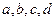 的大小顺序
的大小顺序  ( )
( )