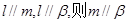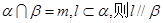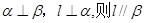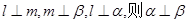题目内容
设f(x)在R上可导,其导数为f′(x),给出下列四组条件:
①p:f(x)是奇函数,q:f′(x)是偶函数;
②p:f(x)是以T为周期的函数,q:f′(x)是以T为周期的函数;
③p:f(x)在区间(-∞,+∞)上为增函数,q:f′(x)>0在(-∞,+∞)恒成立;
④p:f(x)在x0处取得极值,q:f′(x0)=0.
由以上条件中,能使p⇒q成立的序号为 ( ).
①p:f(x)是奇函数,q:f′(x)是偶函数;
②p:f(x)是以T为周期的函数,q:f′(x)是以T为周期的函数;
③p:f(x)在区间(-∞,+∞)上为增函数,q:f′(x)>0在(-∞,+∞)恒成立;
④p:f(x)在x0处取得极值,q:f′(x0)=0.
由以上条件中,能使p⇒q成立的序号为 ( ).
| A.①②③ | B.①②④ | C.①③④ | D.②③④ |
B
由f(-x)=-f(x),得-f′(-x)=-f′(x).∴f′(-x)=f′(x).即f′(x)是偶函数①正确.易知②正确.③不正确.根据f′(x0)=0是可导函数f(x)在x=x0取得极值的必要不充分条件,∴④正确.

练习册系列答案
相关题目
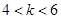 ”是“方程
”是“方程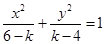 表示椭圆”的
表示椭圆”的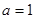 ”是“
”是“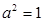 ”的( )
”的( )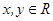 ,则
,则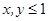 是
是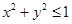 成立的( )
成立的( )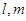 和不重合的两个平面
和不重合的两个平面 ,下列命题正确的是( )
,下列命题正确的是( )