题目内容
12.设曲线x2-y2=0与抛物线y2=-4x的准线围成的三角形区域(包含边界)为D,P(x,y)为D内的一个动点,则目标函数z=x-2y+5的最大值为( )| A. | 4 | B. | 5 | C. | 8 | D. | 10 |
分析 曲线x2-y2=0与抛物线y2=-4x的准线围成的三角形区域,三角形的顶点坐标为(0,0),(1,1),(1,-1),从而可求目标函数z=x-2y+5的最大值.
解答 解:曲线x2-y2=0可化为y=±x,抛物线y2=-4x的准线方程为x=1,
曲线x2-y2=0与抛物线y2=-4x的准线围成的三角形区域,三角形的顶点坐标为(0,0),(1,1),(1,-1)
∴目标函数z=x-2y+5在(1,-1)处,取得最大值为8
故选C.
点评 本题考查函数的最值,考查线性规划知识,确定三角形区域的三角形的顶点坐标是关键.

练习册系列答案
相关题目
6.如图,在棱长为3的正方体ABCD-A1B1C1D1中,点C1到平面A1BD的距离为( )
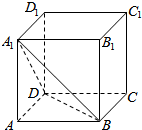

| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |