题目内容
已知a为实数，复数z1＝2－i，z2＝a＋i(i为虚数单位)．
（1）若a＝1，指出
在复平面内对应的点所在的象限；
（2）若z1·z2为纯虚数，求a的值．
（1）第四象限（2）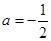
解析试题分析：（1）复数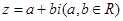
与复平面内点
一一对应，要确定复数在复平面内对应的点所在的象限，关键在于正确求出复数.由于互为共轭的两个复数，实部相等，虚部相反，所以
，因此z1＋
＝(2－i)＋(1－i)＝3－2i，所以z1＋在复平面内对应的点为(3，－2)，在第四象限，（2）复数为纯虚数，有两个条件，一是实部为零，二是虚部不为零.由z1·z2＝(2－i)(a＋i)＝(2a＋1)＋(2－a)i得2a＋1＝0，且2－a≠0，解得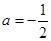
试题解析：
（1）因为a＝1，
所以z1＋＝(2－i)＋(1－i)＝3－2i． 2分
所以z1＋在复平面内对应的点为(3，－2)，
从而z1＋在复平面内对应的点在第四象限． 4分
（2）z1·z2＝(2－i)(a＋i)＝(2a＋1)＋(2－a) i． 6分
因为a∈R，z1·z2为纯虚数，
所以2a＋1＝0，且2－a≠0，解得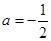． 8分
考点：复数与复平面内点的对应关系，纯虚数概念，共轭复数概念
练习册系列答案
相关题目
与
都是纯虚数，求复数
＋i，ω＝sinθ－icosθ(θ∈R)．求z的值和|z－ω|的取值范围．
—（i—1）a+3b+2i=0
εR,求实数m的值.
及|
在复平面上的对应点在第 象限。