题目内容
已知二次函数f(x)=ax2+bx,且f(x+1)为偶函数,定义:满足f(x)=x的实数x称为函数f(x)的“不动点”,若函数f(x)有且仅有一个不动点,
(1)求f(x)的解析式;
(2)若函数g(x)= f(x)+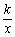 +
+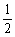 x2在 (0,
x2在 (0, ]上是单调减函数,求实数k的取值范围;
]上是单调减函数,求实数k的取值范围;
(3)在(2)的条件下,是否存在区间[m,n](m<n),使得f(x)在区间[m,n]上的值域为[km,kn]?若存在,请求出区间[m,n];若不存在,请说明理由。
′
解:(1)f(x+1) =a(x+1) 2+b(x+1) = ax 2+(2a+b)x+a+b为偶函数,
∴2a+b=0,∴b=-2a,∴f(x)=ax2-2ax,…………………………………………………………2′
∵函数f(x)有且仅有一个不动点,∴方程f(x)=x有且仅有一个解,∴ax2-(2a+1)x=0有且仅有一个解,∴2a+1=0,a=-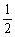 ,∴f(x)= -
,∴f(x)= -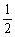 x2+x…………………………………………………5′
x2+x…………………………………………………5′
(2) g(x)= f(x)+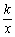 +
+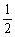 x2=x+
x2=x+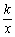 在 (0,
在 (0,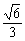 ]上是单调增函数,
]上是单调增函数,
当k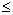 0时,g(x)= x+
0时,g(x)= x+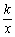 在(0,+
在(0,+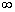 )上是单调增函数,∴不成立;……………………………7′
)上是单调增函数,∴不成立;……………………………7′
当k>0时,g(x)= x+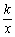 在(0,
在(0,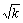 ]上是单调减函数,∴
]上是单调减函数,∴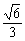
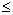
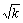 ,∴k
,∴k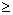
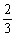 …………………10′
…………………10′
(3) ∵f(x)= -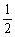 x2+x=
-
x2+x=
-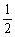 (x-1)2+
(x-1)2+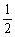
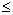
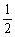 ,∴kn
,∴kn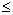
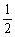 ,∴n
,∴n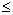
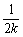
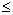
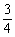 <1,
<1,
∴f(x)在区间[m,n]上是单调增函数…………………………………………………………11′
∴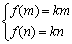 ,即
,即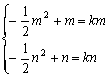 ,方程
,方程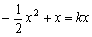 的两根为0,2-2k………………12′
的两根为0,2-2k………………12′
当2-2k>0,即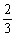
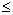 k<1时,[m,n]= [0,2-2k]………………………………………………13′
k<1时,[m,n]= [0,2-2k]………………………………………………13′
当2-2k<0,即k>1时,[m,n]= [2-2k,0]……………………………………………………14′
当2-2k=0,即k=1时,[m,n] 不存在…………………………………………………………15′
