题目内容
4.二进制数101111(2)化为五进制为142(5).分析 先将“二进制”数化为十进制数,然后将十进制的23化为五进制,即可得到结论.
解答 解:先将“二进制”数101111(2)化为十进制数为25+23+22+2+20=47(10)
然后将十进制的47化为五进制:
47÷5=9余2,
9÷5=1余4,
1÷5=0余1,
所以,结果是142(5)
故答案为:142(5).
点评 本题考查的知识点是二进制、十进制与五进制之间的转化,其中熟练掌握“除k取余法”的方法步骤是解答本题的关键.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
14.不等式6${\;}^{({x}^{2}+x-2)}$<1的解集是( )
| A. | (-1,2) | B. | (-2,1) | C. | R | D. | ∅ |
9.已知$\overrightarrow{a}$=(cos40°,sin40°),$\overrightarrow{b}$=(sin20°,cos20°),则$\overrightarrow{a}$•$\overrightarrow{b}$等于( )
| A. | 1 | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
14.双曲线$\frac{x^2}{3}-\frac{y^2}{4}=1$的左焦点到右准线的距离为( )
| A. | $\frac{{3\sqrt{7}}}{7}$ | B. | $\frac{22}{5}$ | C. | $\frac{28}{5}$ | D. | $\frac{{10\sqrt{7}}}{7}$ |
 如图,准备在扇形空地AOB上修建一个山水景观OPQ,己知∠AOB=$\frac{2}{3}$π,OA=lkm,点P在扇形弧上,PQ∥OA交OB于点Q,记∠POA=x.
如图,准备在扇形空地AOB上修建一个山水景观OPQ,己知∠AOB=$\frac{2}{3}$π,OA=lkm,点P在扇形弧上,PQ∥OA交OB于点Q,记∠POA=x.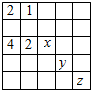 在如图所示的表格中,如果第一格填上一个数后,每一行成等比数列,每一列成等差数列,则x+y+z=2.
在如图所示的表格中,如果第一格填上一个数后,每一行成等比数列,每一列成等差数列,则x+y+z=2.