题目内容
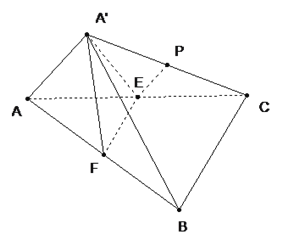
【题目】设直线![]() 与抛物线
与抛物线![]() 相交于不同两点
相交于不同两点![]() 、
、![]() ,与圆
,与圆![]() 相切于点
相切于点![]() ,且
,且![]() 为线段
为线段![]() 中点.
中点.
(1) 若![]() 是正三角形(
是正三角形(![]() 是坐标原点),求此三角形的边长;
是坐标原点),求此三角形的边长;
(2) 若![]() ,求直线
,求直线![]() 的方程;
的方程;
(3) 试对![]() 进行讨论,请你写出符合条件的直线
进行讨论,请你写出符合条件的直线![]() 的条数(直接写出结论).
的条数(直接写出结论).
【答案】(1)![]() (2)
(2)![]() (3)见解析
(3)见解析
【解析】试题分析:(1)若![]() 是正三角形(
是正三角形(![]() 是坐标原点),求出
是坐标原点),求出![]() 的坐标,即可求出此三角形的边长;(2)若
的坐标,即可求出此三角形的边长;(2)若![]() ,设直线
,设直线![]() ,分类讨论,即可求出直线
,分类讨论,即可求出直线![]() 的方程;(3)根据直线与圆的位置关系,可得结论.
的方程;(3)根据直线与圆的位置关系,可得结论.
试题解析:(1)设![]() 的边长为
的边长为![]() ,则
,则![]() 的坐标为
的坐标为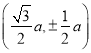
所以![]() 所以
所以![]()
此三角形的边长为![]() .
.
(2)设直线![]()
当![]() 时,
时, ![]() 符合题意
符合题意
当![]() 时,
时, ![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,舍去
,舍去
综上所述,直线![]() 的方程为:
的方程为: ![]()
(3) ![]() 时,共2条;
时,共2条;
![]() 时,共4条;
时,共4条;
![]() 时,共1条.
时,共1条.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目