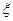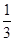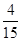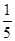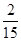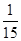Question

（本小题满分12分）甲、乙等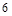名同学参加某高校的自主招生面试，已知采用抽签的方式随机确定各考生的面试顺序（序号为）．

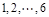（Ⅰ）求甲、乙两考生的面试序号至少有一个为奇数的概率；

（Ⅱ）记在甲、乙两考生之间参加面试的考生人数为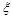，求随机变量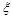的分布列与期望．

 

Answer 1

【答案】

（Ⅰ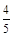）；（Ⅱ）分布列是：

	0	1	2	3	4
P

.

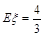【解析】

试题分析：（Ⅰ）用组合计算基本事件数，由等可能性事件的概率计算公式即可求解；（Ⅱ）利用组合也可以求出随机变量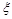的分布列，然后根据期望的定义求出.

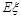（Ⅰ）只考虑甲、乙两考生的相对位置，用组合计算基本事件数；

设A表示“甲、乙的面试序号至少有一个为奇数”，则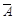表示“甲、乙的序号均为偶数”，

由等可能性事件的概率计算公式得：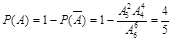

甲、乙两考生的面试序号至少有一个为奇数的概率是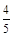.                    6分

（另解）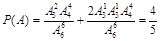

（Ⅱ）随机变量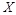的所有可能取值是0，1，2，3，4，

且,,,,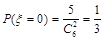

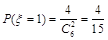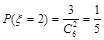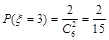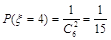
[另解：，，，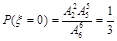

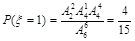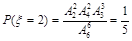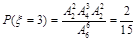
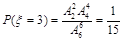                    10分

所以随机变量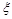的分布列是：

	0	1	2	3	4
P

所以 ，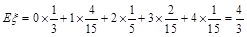

即甲、乙两考生之间的面试考生个数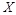的期望值是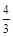.                   12分.

考点：概率知识，分布列和期望的求法.