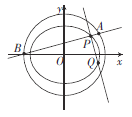
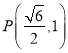题目内容
【题目】抛物线y2=2px(p>0)的焦点为F,已知A,B为抛物线上的两个动点,且满足∠AFB=120°,过弦AB的中点M作抛物线准线的垂线MN,垂足为N,则 ![]() 的最大值为( )
的最大值为( )
A.2
B.![]()
C.1
D.![]()
【答案】D
【解析】解:设|AF|=a,|BF|=b,连接AF、BF, 由抛物线定义,得|AF|=|AQ|,|BF|=|BP|,
在梯形ABPQ中,2|MN|=|AQ|+|BP|=a+b.
由余弦定理得,
|AB|2=a2+b2﹣2abcos120°=a2+b2+ab,
配方得,|AB|2=(a+b)2﹣ab,
又∵ab≤( ![]() )2 ,
)2 ,
∴(a+b)2﹣ab≥(a+b)2﹣ ![]() (a+b)2=
(a+b)2= ![]() (a+b)2
(a+b)2
得到|AB|≥ ![]() (a+b).
(a+b).
所以 ![]() ≤
≤ 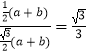 ,
,
即 ![]() 的最大值为
的最大值为 ![]() .
.
故选:D
设|AF|=a,|BF|=b,连接AF、BF.由抛物线定义得2|MN|=a+b,由余弦定理可得|AB|2=(a+b)2﹣ab,进而根据基本不等式,求得|AB|的取值范围,从而得到本题答案.

练习册系列答案
相关题目