题目内容
由直线
上的点向圆
引切线，则切线长的最小值为 .
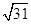
解析试题分析：要使切线长最小，必须直线y=x+2上的点到圆心的距离最小，此最小值即为圆心（4，-2）到直线的距离m，求出m，由勾股定理可求切线长的最小值。解：要使切线长最小，必须直线y=x+2上的点到圆心的距离最小，此最小值即为圆心（4，-2）到直线的距离m，由点到直线的距离公式得 m=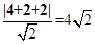
由勾股定理求得切线长的最小值为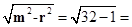 
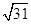,故答案为：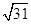
考点：直线和圆的位置关系
点评：本题考查直线和圆的位置关系，点到直线的距离公式、勾股定理得应用．解题的关键是理解要使切线长最小，必须直线y=x+2上的点到圆心的距离最小
练习册系列答案
相关题目
在圆
上，点
关于直线
的对称点也在圆
上，则
。
的圆心是直线
与
轴的交点，且圆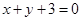
相切.则圆
，过点
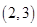的直线
与圆相交于
两点，
,则直线
的长度为1，端点
在边长为2的正方形
的四边上滑动．当
所形成的轨迹为
，若
，则
．
，AB＝3，则切线AD的长为___ _____．
的最短路程是_________.
,直线
,
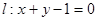的顶点A在直线
上,顶点B、C都在圆M上,且边AB过圆心M,
.则点A横坐标的最大值是 ；