题目内容
用一块钢锭浇铸一个厚度均匀,且全面积为2平方米的正四棱锥形有盖容器(如图),设容器的高为h米,盖子边长为a米.
(1)求a关于h的函数解析式;
(2)设容器的容积为V立方米,则当h为何值时,V最大?求出V的最大值.
(求解本题时,不计容器的厚度)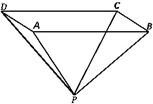
(1)求a关于h的函数解析式;
(2)设容器的容积为V立方米,则当h为何值时,V最大?求出V的最大值.
(求解本题时,不计容器的厚度)

(1)设h'为正四棱锥的斜高
由已知
解得a=
(h>0)
(2)V=
ha2=
(h>0)
易得V=
因为h+
≥2
=2,所以V≤
等式当且仅当h=
,即h=1时取得.
故当h=1米时,V有最大值,V的最大值为
立方米.
由已知
|
解得a=
| 1 | ||
|
(2)V=
| 1 |
| 3 |
| h |
| 3(h2+1) |
易得V=
| 1 | ||
3(h+
|
因为h+
| 1 |
| h |
h?
|
| 1 |
| 6 |
等式当且仅当h=
| 1 |
| h |
故当h=1米时,V有最大值,V的最大值为
| 1 |
| 6 |

练习册系列答案
相关题目