题目内容
判断题：
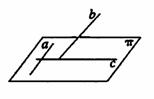
（1） 一条直线垂直于一个平面内的两条平行直线，这条直线垂直于这个平面；
（2） 如果三条直线共点，且两两垂直，其中一条直线垂直于另两条直线所确定的平面．
（1） 一条直线垂直于一个平面内的两条平行直线，这条直线垂直于这个平面；
（2） 如果三条直线共点，且两两垂直，其中一条直线垂直于另两条直线所确定的平面．
分析：（1）对照直线与平面垂直的判定定理的诸多条件，然后进行判定即可；
（2）根据直线与平面垂直的判定定理，找出定理所需条件进行判定即可．
（2）根据直线与平面垂直的判定定理，找出定理所需条件进行判定即可．
解答：解：（1）对照线面垂直的判定定理“一条直线垂直于平面内两条相交直线，则这条直线垂直于这个平面”可知原命题不正确；
（2）如果三条直线共点，且两两垂直，则一条直线垂直于另两条相交直线，则垂直于另两条直线所确定的平面．故原命题正确．
（2）如果三条直线共点，且两两垂直，则一条直线垂直于另两条相交直线，则垂直于另两条直线所确定的平面．故原命题正确．
点评：本题主要考查了直线与平面垂直的判定，应熟练记忆直线与平面垂直的判定定理，属于基础题．
练习册系列答案
相关题目
是平面
内的一条直线，
是
是直线
，则
”为真。