题目内容
本小题满分12分
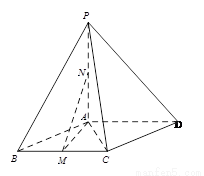
如图,在直三棱柱ABC—A1B1C1中,AC=1,AB= ,BC=
,BC= ,AA1=
,AA1= 。
。
(I)求证:A1B⊥B1C;
(II)求二面角A1—B1C—B的大小。

【答案】
I)由AC=1,AB=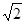 ,BC=
,BC= 知AC2+AB2=BC2,
知AC2+AB2=BC2,
所以AC⊥AB。
因为ABC—A1B1C1是直三棱柱,面ABB1A1⊥面ABC,
所以AC⊥面ABB1A1。………………3分
由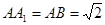 ,知侧面ABB1A1是正方形,连结AB1,
,知侧面ABB1A1是正方形,连结AB1,
所以A1B⊥AB1。
由三垂线定理得A1B⊥B1C。 ………………6分
(II)作BD⊥B1C,垂足为D,连结A1D。
由(I)知,A1B⊥B1C,则B1C⊥面A1BD,
于是B1C⊥A1D,
则∠A1DB为二面角
A1—B1C—B的平面角。 ………………8分
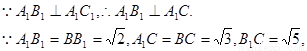
∴Rt△A1B1C≌Rt△B1BC,
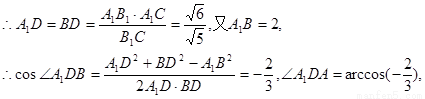
故二面角A1—B1C—B的大小为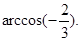 ………………12分
………………12分
【解析】略

练习册系列答案
相关题目
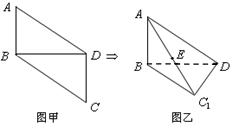
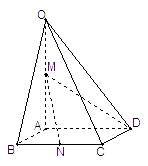 如图,在四棱锥
如图,在四棱锥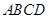 中,
中,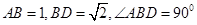 ,将它们沿对角线
,将它们沿对角线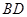 折起,折后的点
折起,折后的点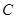 变为
变为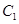 ,且
,且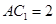 .
.
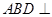 平面
平面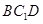 ;
;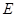 为线段
为线段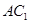 上的一个动点,当线段
上的一个动点,当线段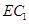 的长为多少时,
的长为多少时, 与平面
与平面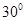 ?
?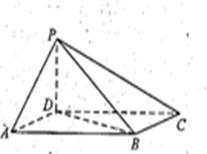
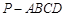 中,底面
中,底面 是菱形,
是菱形,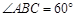 ,
,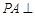 平面
平面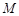 、
、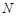 分别为
分别为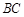 、
、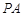 的中点,
的中点,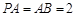 .
. 平面
平面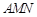 ;
;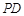 上是否存在一点
上是否存在一点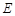 ,使得
,使得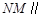 平面
平面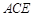 ;若存在,求出
;若存在,求出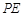 的长;若不存在,请说明理由。
的长;若不存在,请说明理由。