题目内容
设正数x,y满足x+4y=40,则lgx+lgy的最大值是( )
| A.2 | B.10 | C.4 | D.40 |
∵x+4y=40,
∴40=x+4y≥2
,
即xy≤100,当且仅当x=4y=20取等号.
∴lgx+lgy=lgxy≤lg100=2.
故lgx+lgy的最大值是2.
故选:A.
∴40=x+4y≥2
| 4xy |
即xy≤100,当且仅当x=4y=20取等号.
∴lgx+lgy=lgxy≤lg100=2.
故lgx+lgy的最大值是2.
故选:A.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
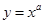 的图象过点
的图象过点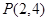 ,则图中阴影部分的面积等于 .
,则图中阴影部分的面积等于 .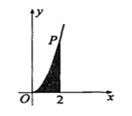
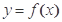 的图象经过点
的图象经过点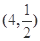 ,则
,则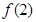 ( )
( )