题目内容
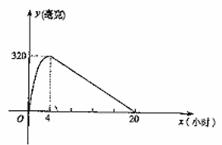
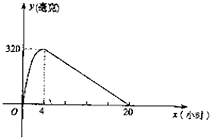 某种新药服用x小时后血液中的残留量为y毫克,如图为函数y=f(x)的图象,当血液中药物残留量不小于240毫克时,治疗有效.
某种新药服用x小时后血液中的残留量为y毫克,如图为函数y=f(x)的图象,当血液中药物残留量不小于240毫克时,治疗有效.(I)求函数y=f(x)的解析式;
(II)设某人上午8:00第一次服药,为保证疗效,试分别计算出第二次、第三次服药的时间.
分析:(Ⅰ)由图象分段设出一次函数模型,分别代入点(4,320)和(20,0)求解函数解析式;
(Ⅱ)设x为第一次服药后经过的时间,由第一次服药的残留量大于等于240求解x的范围,同样由第二次服药的残留量大于等于240求解第二次的药效时间,再由前两次的服药残留量大于240求解第三次的服药时间.
(Ⅱ)设x为第一次服药后经过的时间,由第一次服药的残留量大于等于240求解x的范围,同样由第二次服药的残留量大于等于240求解第二次的药效时间,再由前两次的服药残留量大于240求解第三次的服药时间.
解答:解:(I)由图象可知:
当x∈[0,4]时,设y=kx.
把(4,320)代入,得k=80,∴y=80x.
当x∈[4,320]时,设y=kx+b.
把(4,20),(20,0)代入得
,解得
.
∴y=400-20x.
∴f(x)=
(II)设x为第一次服药后经过的时间,
则第一次服药的残留量y1=f(x)=
由y1≥240,得
或
解得3≤x≤4或4<x≤8,∴3≤x≤8.
故第二次服药应在第一次服药8小时后,即当日16:00.
设第二次服药产生的残留量为y2,
则y2=f(x-8)=
由y2≥240,得
或
解得11≤x≤12或12<x≤16,∴11≤x≤16.
若仅考虑第二次服药的残留量,第三次服药应在第一次服药16小时后,而前两次服药的残留量为
y1+y2,由
得
,解得16<x≤18.
故第三次服药应在第一次服药18小时后,即次日凌晨2:00.
当x∈[0,4]时,设y=kx.
把(4,320)代入,得k=80,∴y=80x.
当x∈[4,320]时,设y=kx+b.
把(4,20),(20,0)代入得
|
|
∴y=400-20x.
∴f(x)=
|
(II)设x为第一次服药后经过的时间,
则第一次服药的残留量y1=f(x)=
|
由y1≥240,得
|
|
解得3≤x≤4或4<x≤8,∴3≤x≤8.
故第二次服药应在第一次服药8小时后,即当日16:00.
设第二次服药产生的残留量为y2,
则y2=f(x-8)=
|
由y2≥240,得
|
|
解得11≤x≤12或12<x≤16,∴11≤x≤16.
若仅考虑第二次服药的残留量,第三次服药应在第一次服药16小时后,而前两次服药的残留量为
y1+y2,由
|
得
|
故第三次服药应在第一次服药18小时后,即次日凌晨2:00.
点评:本题考查了函数模型的选择及应用,考查了分段函数涉及的不等式的解法,解答此题的关键是对题意的理解与把握,考查了计算能力,是中档题.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
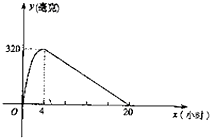 某种新药服用x小时后血液中的残留量为y毫克,如图为函数y=f(x)的图象,在x∈(0,4]时为二次函数,且当x=4时到达顶点;在x∈(4,20]为一次函数,当血液中药物残留量不小于240毫克时,治疗有效.
某种新药服用x小时后血液中的残留量为y毫克,如图为函数y=f(x)的图象,在x∈(0,4]时为二次函数,且当x=4时到达顶点;在x∈(4,20]为一次函数,当血液中药物残留量不小于240毫克时,治疗有效.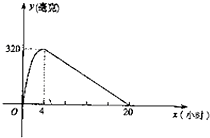 某种新药服用x小时后血液中的残留量为y毫克,如图为函数y=f(x)的图象,当血液中药物残留量不小于240毫克时,治疗有效.
某种新药服用x小时后血液中的残留量为y毫克,如图为函数y=f(x)的图象,当血液中药物残留量不小于240毫克时,治疗有效.