题目内容
【题目】设常数![]() ,函数
,函数![]()
(1)当![]() 时,判断
时,判断![]() 在
在![]() 上单调性,并加以证明;
上单调性,并加以证明;
(2)当![]() 时,研究
时,研究![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(3)当![]() 时,若存在区间
时,若存在区间![]() 使得
使得![]() 在
在![]() 上的值域为
上的值域为![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() 在
在![]() 上是单调递增.证明见解析(2)见解析;(3)
上是单调递增.证明见解析(2)见解析;(3)![]()
【解析】
(1)由函数的单调性定义即可证明。
(2)由函数的奇偶性定义即可证明。
(3)首先证明函数的单调性,当![]() 时证明函数
时证明函数![]() 在
在![]() 上单调递增,即
上单调递增,即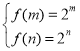 ,解关于
,解关于![]() 一元二次方程即可;
一元二次方程即可;
同理当![]() 时,求出
时,求出![]() 单调区间,当函数是单调递减时,则
单调区间,当函数是单调递减时,则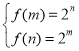 代入化简即可求解。
代入化简即可求解。
解:(1)当![]() 时,
时,![]()
任取![]()
则![]()
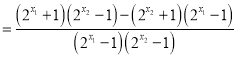
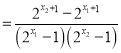
∵![]()
∴![]()
∴![]()
∴![]()
∵![]() ,
,![]()
∴![]() ,
,![]()
∴![]() ,
,![]()
∴![]()
即:![]()
∴![]() 在
在![]() 上是单调递增.
上是单调递增.
(2)①当![]() 时,
时,![]()
∵![]()
∴![]() 为偶函数
为偶函数
②当![]() 时,
时,![]()
![]() ,则
,则![]()
![]() 当
当![]() 且
且![]() 时,
时,![]() 的定义域为
的定义域为![]()
定义域不关于原点对称
∴![]() 为非奇非偶函数
为非奇非偶函数
![]() 当
当![]() 时,
时,![]() ,
,![]() 的定义域为
的定义域为![]()
定义域关于原点对称
![]()
∴![]() 为奇函数.
为奇函数.
(3)①当![]() 时,
时,![]() 定义域为
定义域为![]()
![]()
∵![]() 单调递增,∴
单调递增,∴![]() 单调递减
单调递减
∴![]() 在
在![]() 上单调递增
上单调递增
由题意得: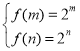
∴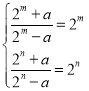
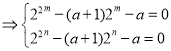
∴![]() ,
,![]() 是一元二次方程:
是一元二次方程:
![]() 的两个不等的正根
的两个不等的正根
∴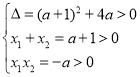
![]()
②当![]() 时,
时,![]() 定义域为
定义域为![]()
∵当![]() 时,
时,![]() 的值域为
的值域为![]()
∴![]() ,
,![]()
当![]() 时,
时,![]()
∵![]() 单调递增,∴
单调递增,∴![]() 单调递减
单调递减
∴![]() 在
在![]() 上单调递减
上单调递减
∴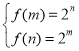
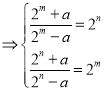
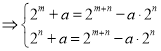
∴![]()
∵![]()
∴![]()
∴![]()
综上所述:![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
相关题目
【题目】众所周知,大型网络游戏(下面简称网游)的运行必须依托于网络的基础上,否则会出现频繁掉线的情况,进而影响游戏的销售和推广,某网游经销在甲地区5个位置对两种类型的网络(包括“电信”和“网通”)在相同条件下进行游戏掉线的测试,得到数据如下:
位置 类型 | A | B | C | D | E |
电信 | 4 | 3 | 8 | 6 | 12 |
网通 | 5 | 7 | 9 | 4 | 3 |
(1)如果在测试中掉线次数超过5次,则网络状况为“糟糕”,否则为“良好”,那么在犯错误的概率不超过0.15的前提下,能否说明网络状况与网络的类型有关?
(2)若该游戏经销商要在上述接受测试的电信的5个地区中任选2个作为游戏推广,求A,B两地区至少选到一个的概率.
参考公式: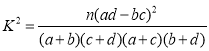 .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|