题目内容
【题目】若圆锥的内切球(球面与圆锥的侧面以及底面都相切)的半径为1,当该圆锥体积取最小值时,该圆锥体积与其内切球体积比为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
解法一:设圆锥底面半径为![]() ,高为
,高为![]() ,根据
,根据![]() ∽
∽![]() 可得
可得![]() ,即
,即![]() ,利用锥体的体积公式
,利用锥体的体积公式![]() ,然后利用基本不等式求最值;解法二:同解法一,利用导数求最值;解法三:设
,然后利用基本不等式求最值;解法二:同解法一,利用导数求最值;解法三:设![]() ,可得
,可得![]() ,
,![]() ,即
,即![]() ,设
,设![]() ,利用二次函数配方即可求解.
,利用二次函数配方即可求解.
解法一:如图,设圆锥底面半径为![]() ,高为
,高为![]() .
.
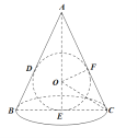
由![]() ∽
∽![]() 可得
可得![]() ,即
,即![]() ,
,
则![]() ,
,
所以![]() ,
,
因为![]() ,所以
,所以![]() ,当且仅当
,当且仅当![]() ,即
,即![]() 时取等号,
时取等号,
此时圆锥体积最小,最小值为![]() .因为该球的体积为
.因为该球的体积为![]() ,
,
所以该圆锥体积与其内切球体积比为![]() .
.
解法二: 如图,设圆锥底面半径为![]() ,高为
,高为![]() .
.

由![]() ∽
∽![]() 可得
可得![]() ,即
,即![]() ,
,
则![]() ,
,
所以![]() 令
令![]() ,
,
则![]() ,
,
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,所以
上单调递增,所以![]() ,
,
即![]() 时,该圆锥体积最小, 最小值为
时,该圆锥体积最小, 最小值为![]() .又其内切球体积为
.又其内切球体积为![]() .
.
所以该圆锥体积与其内切球体积比为![]() ,
,
解法三:设![]() ,则
,则![]() ,所以
,所以![]() ,
,
又![]()
![]() ,所以
,所以![]() ,
,
所以![]() ,令
,令![]() ,
,
因为![]() ,当且仅当
,当且仅当![]() 时取得最大值
时取得最大值![]() ,
,
从而圆锥体积最小,最小值为![]() .因为该球的体积为
.因为该球的体积为![]() ,
,
所以该圆锥体积与其内切球体积比为![]() ,
,
故选:D.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目